La vecindad de von Neumann diseñada con la idea de optimizar espacio, tiene un
traslape que difiere en gran medida al traslape de la vecindad de Moore. Para empezar, la
vecindad de von Neumann está definida por las siguientes 5 células: (i,j),(i,j+1),(i,j-1),(i+1,j),(i-1,j),
con un poco más de la mitad de células que la vecindad de Moore, diferencia considerable
que se irá incrementando rápidamente conforme aumenta la dimensión.
En el caso de la vecindad de von Neumann sólo tiene vecinos ortogonales, de forma que el
único traslape a considerar es el ortogonal. Bajo ésta consideración el traslape en dos
dimensiones ocurre en las células (i,j),(i+1,j) (como lo ilustra la figura 5) entre las 7 que constituyen el total de células de la
vecindad, dando un traslape de 2/7 La vecindad de von Neumann en tres dimensiones
consta de 7 células ((i,j,k),(i+1,j,k),(i-1,j,k),(i,j+1,k),(i,j-1,k),(i,j,k+1),(i,j,k-1))
esto equivale aproximadamente a 1/4 con respecto a la vecindad de Moore. En tres
dimensiones el traslape se da en 2 células: (i,k,j),(i,j,k+1) de un total de 7
como se puede apreciar en la gráfica 6; de manera
que 2/7 es el grado de traslape en 3 dimensiones.
En general se puede observar que existen dos células en cada dimensión del conjunto de
células que forman a la vecindad y una célula (la célula central) que llega a ser parte
de todas las direcciones involucradas (espacios). De manera que el número de células que
tiene una vecindad de von Neumann en n dimensiones es:
![]()
para los casos n=2 y n=3, se puede constatar el número de células 2(2)+1=5 y 2(3)+1=7 respectivamente, con lo expuesto apenas unos párrafos arriba.
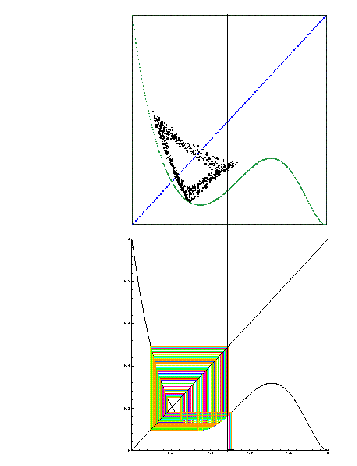
Figura 7: a) Arriba: Despliegue del mapa de retorno de las densidades
reales del autómata celular (2.3), con regla de evolución 33. b) Abajo: Graficación de
la escalera sobre la iteración de la aproximación del campo promedio, en tres
dimensiones.
Los traslapes en tres dimensiones en la vecindad de von Neumann se dan a través de las
células alineadas ortogonalmente en cada dirección. Si se recorre una célula sobre el
eje de cualquier dimensión se tendrán 3-1=2 traslapes, ya que 3 es el número de
células por cada eje, cualquiera que este sea. Y además los traslapes en todas las
dimensiones restantes desaparecen, por lo que para cualquier dimensión el traslape será
de:
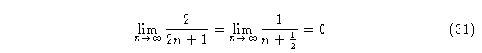
Es decir que el traslape disminuye cuando la dimensión aumenta.
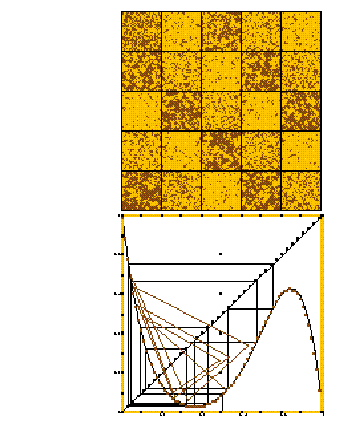
Figura 8: a) Arriba: Despliegue de la evolución del Autómata celular
(2.4), en el plano con regla 385. b) Abajo: Aproximación del campo promedio (graficación
de la escalera) contra la composición de funciones (gráfica triángular) en 4
dimensiones.