The maximal first stage de Bruijn diagram has 64 nodes connected by 512
links. The nodes are representable by a pair of octal numbers or
equivalently, by a single number modulo 64. In that case, it is easy to
describe the connectivity matrix 
, whose elements are defined by
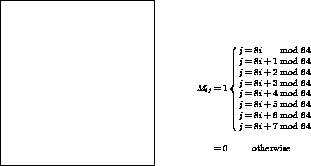
Figure 1: the full first stage 
de Bruijn matrix
This matrix is shown in greater detail in Figure 1.
By inspection, 
and 
is a matrix solidly filled with
1's. Therefore 
and M satisfies the minimal equation
from which its characteristic equation can be obtained. It is evident from calculating traces of its powers that there are many loops of all possible lengths in the diagram. There are also numerous Hamiltonian loops, these latter passing through all 64 different nodes, giving the longest possible consecutive sequences of neighborhoods that can be formed without repeating one of them.
Dropping links from the complete de Bruijn diagram will break some loops, maybe even isolate certain nodes completely. Normally such artifacts would be discarded; if a node had no exit links, it would mean that there was a partial neighborhood for which no right border existed so that the central cell would remain constant in the next generation. Such partial neighborhoods are barriers to extending a region of still lifes, therefore inappropriate to an infinite plane.
Such barriers would terminate any recursion reaching them in the direct approach to still lifes; the advantage of using de Bruijn diagrams is just that their occurrence is clearly located in the context of the finite number of distinct sequences of neighborhoods which exist.
Although emphasis has been placed on still lifes, it should be noted
that the evolved cell can be compared to any of the other cells in the
neighborhood from which it arose, not just the original cell. The
simplest comparisons are with the shifted cells; by symmetry the
interesting ones would be the longitudinal neighbor in the direction of
progressive overlapping, the transversal neighbor perpendicular to the
direction of extension, and the diagonal neighbor. Using the symbol
to designate a pattern in which a cell matches the one x
cells to the right and y cells up after t generations, the fundamental
neighborhood is large enough to detect the patterns (0,0,1), (0,1,1),
(1,0,1), and (1,1,1). The first of these are the still lifes, the
others might be called gliders. Strictly, Conway's glider corresponds
to the pattern (1,1,4), his space ships to (0,2,4) or (2,0,4).
In principle any Boolean combination of the evolved cell with the cells of its neighborhood could form the basis of a pattern. For example, a pattern could consist of configurations which vanished after a single generation.
Figure 2: the de Bruijn matrix for Life 's still lifes
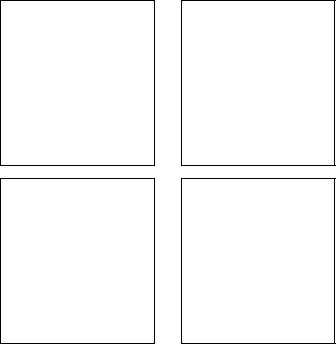
Figure 3: second through fifth powers of the de Bruijn matrix
Figure 2 shows the connection matrix of the first stage de Bruijn diagram for still lifes, from which its resemblance to the complete diagram can be judged. A better understanding can be formed by inspecting several of the lower powers of the matrix, as shown in Figure 3 on the next page.
The block structure of M is evident by the power 
; the fact that
is still fairly sparse but 
is not indicates the presence of
an important component of period 3. This situation has been strongly
evident to those who have examined large empirical collections of still
lifes, among which the length three is a magic number. In terms of the
properties of positive matrices, an explanation would be that the second
largest eigenvalue was triply degenerate (in absolute value).
Although there is probably no real ``explanation'' of why 3 is magic,
those who have worked with Life have noticed that the still lifes for
a 
torus are just those configurations with four live cells,
an easy requirement to satisfy. The same rule works for a general 
torus, although an additional family of still lifes is also
possible. Apparently breaking the periodicity in the cross direction
still leaves ample opportunity to form still lifes. It would be
interesting to know whether this phenomonon persists for other rules or
for other lattices.
The ergodic set of the diagram has 57 nodes, the remaining seven never appearing in any still life. This is not surprising, since it is foreordained that the live central cell in neighborhood built either by extending the nodes 73, 76, or 77 to the right, or the nodes 37, 67, or 77 to the left will die. The node 57 cannot be extended to the right, nor 75 to the left, but each can be extended in the other direction. They, too, have to be removed from the diagram.
Usually the exclusion of nodes is more subtle, requiring much higher powers of the connectivity matrix to establish the pattern clearly.
Although relatively few nodes are lacking from the full de Bruijn diagram, about half the links are missing. In general such numbers are explained by the fact that there are two classes of neighborhoods, the good and the bad, and that they occur in roughly equal numbers. Thus there is a 50% probability of dropping any given link from the diagram.
Eight links must be dropped to leave a node without exit links; since
, there is about 0.4% chance of
finding one such node, which means that not too many bare nodes will be
found among 64. The fact that seven are missing has to be considered as
a fluctuation, due to some special characteristic of Conway's game.
Experience with other rules tends to confirm this evaluation.
Similarly rough estimates apply to the chance of finding loops; we
expect 
loops of length N (with repeated subloops included) but
cutting any link ruins the loop, so that there is one chance in 
of finding an intact loop of that length. Thus the expectation is that
the number of loops will quadruple with any increment in length. The
dominant eigenvalue of the de Bruijn matrix gives the most accurate
estimate of this factor, which is generally close to 4.0.
The following table presents the number of loops originating with the quiescent state, the total number of loops, and the maximum number possible. Bear in mind that the trace of the connection matrix counts a loop once for each node which it contains, but not multiple traverses of portions of a loop, so the crude data does not reflect the usual number of cycles as they are commonly counted.
This data shows that the number of loops is multiplied by approximately four for each increment in length, and that there is a strong component of period 3; as confirmed by experimental tallies of the number of still lifes.