![]()
El estudio sobre autómatas celulares reversibles no ha sido resuelto en su totalidad hasta nuestros días para todos los casos posibles, sin embargo se han logrado avances muy importantes que nos han permitido comprender de una manera más clara la explicación de este comportamiento. Mencionaremos de manera general las características más importantes para identificar autómatas celulares reversibles.
Los autómatas celulares reversibles se caracterizan por tener un mapeo inyectivo y a
la vez suryectivo, es decir tienen un mapeo biyectivo, carecen de configuraciones
pertenecientes al Jardín del Edén y tampoco tienen múltiples ancestros. Esto significa
que los árboles topológicos estan constituidos sólo de puras raíces cíclicas, no
existen ramas ni hojas. Trabajaremos con un autómata ![]() para tener una idea más clara de estos
conceptos.
para tener una idea más clara de estos
conceptos.
El autómata celular de la Figura 4.1 ilustra algunas condiciones básicas para detectar si el autómata es reversible o no. Mencionaremos sólo algunas pues este estudio se ha desarrollado detalladamente en [21].
Una primera condición es que los estados deben existir en igual número en el diagrama de de Bruijn, esto es, debe de cumplir el teorema de Múltiplicidad Uniforme [2] [16] [11] que nos dice; si tenemos un estado con un número de ancestros igual al número de nodos del diagrama de de Bruijn, entonces para toda concatenación que realizemos por la izquierda o por la derecha el número de ancestros debe ser el mismo.
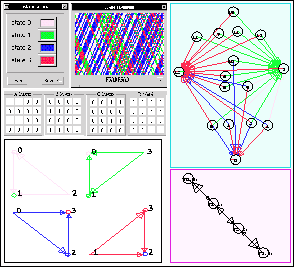
Figura: Autómata reversible ![]() regla F5A0F5A0.
regla F5A0F5A0.
La segunda implica que en el diagrama de subconjuntos no deben existir cadenas que vayan del conjunto máximo al conjunto mínimo y además que no existan secuencias de estados que formen ciclos dentro de las mismas clases unitarias, ya que las secuencias deben estacionarse en una clase unitaria del diagrama sin pasar a otra clase unitaria, es decir, estacionarse en un sólo nivel o en su defecto llegar de un sólo paso al conjunto máximo o al conjunto mínimo. Esta propiedad va asociada a la primera condición ya que si el autómata cumple con el teorema de múltiplicidad uniforme, también debe cumplir con el teorema de los Índices de Welch [2] [16] [11] que nos dice; si todas las secuencias posibles que se encuentran dentro de las clases unitarias que describen los mismos índices de Welch ya sea por la izquierda o por la derecha, forman cadenas de longitud mayor igual que uno y menor igual al número de nodos del diagrama de de Bruijn, esto nos indica que debe existir un único ancestro.
La tercera propiedad es analizar el diagrama de parejas que nos ayuda a verificar la nula existencia de ciclos fuera de la diagonal principal, es decir no existen múltiples ancestros. Los ciclos que existen dentro de la diagonal principal se debe por que los nodos de la diagonal principal no son más que los mismos nodos del diagrama de de Bruijn.
Regresando a la Figura 4.1 podemos identificar estas propiedades mencionadas en el párrafo anterior, las matrices de conectividad derivadas del diagrama de de Bruijn por estado, contienen el mismo número de elementos por cada uno de los estados posibles, lo que implica que en el diagrama de de Bruijn deben existir igual número de aristas por cada uno de los estados. El diagrama de subconjuntos muestra todas las posibles secuencias originadas desde cualquier nodo, es decir con sus cuatro clases unitarias construidas. Si seguimos cualquier secuencia podemos verificar como de la clase unitaria uno sube a la clase unitaria dos o baja al conjunto vacio, la clase unitaria tres sólo baja a la clase unitaria dos, la clase unitaria cuatro baja a los nodos 12 y 3 de la clase unitaria dos, a estos nodos también se les conoce como nodos atractores. Por lo que deducimos que la clase unitaria nivel dos es la clase que contiene las propiedades de los índices de Welch y cumple con la propiedad de que toda secuencia que exista dentro de esta clase debe de ser mayor igual a uno y menor igual al número de nodos del diagrama de de Bruijn. Finalmente podemos verificar que el autómata presenta un mapeo biyectivo y carece de múltiples ancestros ya que se a gráficado su respectivo diagrama de parejas con la opción sólo ciclos y observamos que no existen ciclos fuera de la diagonal principal con lo que se determina que el autómata celular es reversible.
Existen aún más sutilezas por analizar, pero este no es el fin de esta sección. Si se desea un mayor análisis de estas propiedades se puede consultar la siguiente bibliografía [2] [16] [20] [11] [10] [21], donde se desarrolla con gran profundidad y de manera formal la demostración y representación de tales teoremas.
![]()