El autómata celular 
regla 016ED4BB presenta grados de reversibilidad para configuraciones que no sean
múltiplos de tres. En primer instancia obtengamos los productos matriciales por estado
para determinar si alguno de los cuatro estados determina la reversibilidad para este
autómata.
Primeramente construyamos sus matrices de conectividad.
Todas las matrices cumplen con la condición de que su traza es igual a uno, lo que significa que las configuraciones de tamaño uno tienen un único ancestro. Ahora analizaremos cada uno de los estados y sus respectivas potencias.
Las matriz 
elevada a
una n-ésima potencia es idempotente para toda 
, por lo que para toda cadena formada por el
estado 00*, esta cadena va a tener un único ancestro.
La matriz de conectividad 
alcanza la idempotencia cuando 
, y conserva la 
para cualquer potencia de 
.
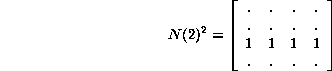
Para el estado 2 su matriz de conectividad alcanza rápidamente la idempotencia cuando n=2. Mostrando un único ancestro para configuraciones 22*.
La matriz 
alcanza la
idempotencia cuando 
igual
que el estado 1 y la 
lo
que confirma un único ancestro para toda configuración formada por la cadena 33*.
Todo parece indicar que el autómata celular es reversible para todas las configuraciones de tamaño par e impar. Sin embargo si análizamos su diagrama de parejas veremos que no es reversible.
Figura 4.10: Diagrama de parejas de la regla 016ED4BB.
La Figura 4.10 ilustra la existencia de ciclos fuera de la diagonal, lo que implica que
este autómata celular no es reversible. La explicación de este fénomeno es que los
ciclos se forman por cadenas que estan formadas por combinaciones de los mismos estados.
Si efectuamos todas las combinaciones posibles cuando l=2, entonces tenemos
dieciseis casos posibles donde la 
.
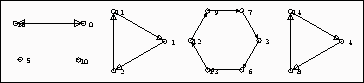
Figura 4.11: Árboles topológicos con l=2.
La Figura 4.11 ilustra todas las configuraciones 
donde el mapeo global es biyectivo y lógicamente
támbien es reversible para este valor. Por que sólo existe una configuración que
construye a otra configuración para todos los estados globales que podemos formar con l=2.
Los ciclos 5 y 10 son de longitud uno, esto quiere decir que la evolución para este caso
va a ser siempre 5 ó 10 en todo el diagrama de evoluciones.
Ahora analizemos la secuencia formada por los estados 123 donde sus productos matriciales los representamos de la siguiente manera:
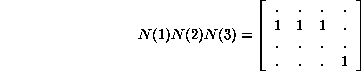
podemos ver que la 
lo
que implica que la configuración tiene dos ciclos que a su vez indican dos ancestros para
dicha cadena. Estas cadenas estan formadas por los bloques de evolución 1221 y 3013, sus
ancestros de la cadena 123 son los estados 221 y 013 respectivamente.
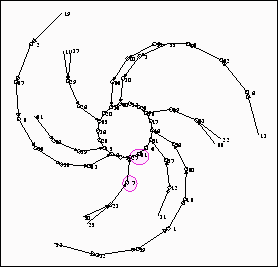
Figura 4.12: Diagrama de transiciones con l=3.
La Figura 4.12 ilustra uno de los árboles topológicos cuando l=3 y podemos verificar que la cadena 123 representada por el estado global 27 tiene dos ancestros, los estados globales 41 y 7 representadas por las cadenas 221 y 013 respectivamente.
Por lo que deducimos que para determinar los grados de reversibilidad de un ancho
específico tenemos que efectuar todas las combinaciones posibles determinadas por k.
Y el orden de n determinará el tamaño de l para toda configuración 
.
Comprobando los grados de reversibilidad para este autómata revisemos la secuencia 102303 que debe de tener más de un ancestro, ya que l es un múltiplo de tres en este caso.
La matriz de conectividad para la cadena representada por los estados 102303 presenta
una 
lo que implica que
dicha configuración posee dos ancestros y no es reversible cuando l=6.