| g3:y | (2+y)2 | ||
| gn2y+1(y+1) | (6) |
En efecto, demostrémosla por inducción en n. Caso ``base'': Para n=3 se tiene
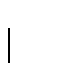 se cumple 2.8. Entonces
se cumple 2.8. Entonces
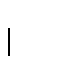 es creciente respecto a su índice n, i.e.
es creciente respecto a su índice n, i.e.  .
f1 es la función suma, luego
.
f1 es la función suma, luego
 se comprueba inmediatamente que
se comprueba inmediatamente que
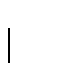 .
Supongamos
.
Supongamos
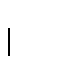 ,
cualquiera que sea y. Mostrémosla para x+1:
,
cualquiera que sea y. Mostrémosla para x+1: