Problema 2.1 (de deducción)
Para un conjunto definible
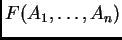
y un objeto dado
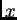
, si se sabe que cada grado de pertenencia
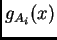
cae en un intervalo
![$[a_i,b_i]$](img70.png)
, entonces se ha de estimar en qué intervalo
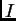
ha de caer el grado de pertenencia
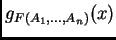
.
Problema 2.2 (de inferencia)
Para un conjunto definible
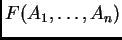
y un objeto dado
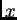
, si se sabe que el grado de pertenencia
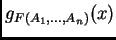
cae en un intervalo
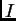
, y que para algunos conjuntos primitivos
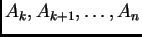
sus correspondientes grados de pertenencia
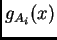
caen en intervalos
![$[a_i,b_i]$](img70.png)
,
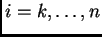
, entonces se ha de estimar para los otros índices
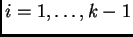
en qué intervalos
![$[a_i,b_i]$](img70.png)
debieron caer los correspondientes grados de pertenencia
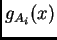
.