



Siguiente: Autómatas de pila con
Un nivel arriba: Autómatas de pila
Anterior: Autómatas de pila y
Un autómata de pila determinista es un autómata de pila
donde se cumplen las siguientes dos propiedades:
- Para cualquier pareja (estado,tope_de_la_pila) se tiene que o bien el autómata tiene definida la transición correspondiente a la palabra de entrada vacía o bien la tiene definida en símbolos del alfabeto de entrada, y
- para cualquier terceta (estado,s,tope_de_la_pila), la transición correspondiente contiene, a lo sumo, una pareja (nuevo_estado,tope_de_la_pila).
En símbolos,
Sea
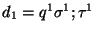 un autómata de pila determinista. De acuerdo con la construcción vista para obtener la gramática libre de contexto de un autómata de pila dado, tendremos que las producciones de la gramática correspondiente han de ser las siguientes:
un autómata de pila determinista. De acuerdo con la construcción vista para obtener la gramática libre de contexto de un autómata de pila dado, tendremos que las producciones de la gramática correspondiente han de ser las siguientes:
- 1.
-
![$\forall q\in Q:\ S\rightarrow [q_0,X,q]$](img1752.gif)
- 2.
-

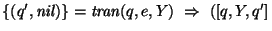
para cualesquiera selecciones de los estados
 .
.
- 3.
-

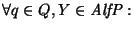
para cualesquiera selecciones de los estados
 .
.
- 4.
-

![$\{(q',\mbox{\it nil\/})\}=\mbox{\it tran\/}(q,e,Y)\ \Rightarrow\ \left([q,Y,q']\rightarrow e\right)$](img1817.gif) .
.
- 5.
-
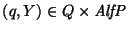
![$\{(q',\mbox{\it nil\/})\}=\mbox{\it tran\/}(q,\mbox{\it nil\/},Y)\ \Rightarrow\ \left([q,Y,q']\rightarrow \mbox{\it nil\/}\right)$](img1819.gif) .
.
En este caso, si para una pareja
 se generasen producciones de acuerdo con la regla 3 entonces no se generará ninguna con la regla 2. Similarmente, si se generase una con la 5, no se generarará ninguna con la 4.
De aquí resulta que cualquier lenguaje reconocido por una autómata de pila determinista ha de ser generado por una gramática libre de contexto cuyas producciones son de la forma
se generasen producciones de acuerdo con la regla 3 entonces no se generará ninguna con la regla 2. Similarmente, si se generase una con la 5, no se generarará ninguna con la 4.
De aquí resulta que cualquier lenguaje reconocido por una autómata de pila determinista ha de ser generado por una gramática libre de contexto cuyas producciones son de la forma




Siguiente: Autómatas de pila con
Un nivel arriba: Autómatas de pila
Anterior: Autómatas de pila y
Guillermo Morales-Luna
2000-06-27
 se generasen producciones de acuerdo con la regla 3 entonces no se generará ninguna con la regla 2. Similarmente, si se generase una con la 5, no se generarará ninguna con la 4.
De aquí resulta que cualquier lenguaje reconocido por una autómata de pila determinista ha de ser generado por una gramática libre de contexto cuyas producciones son de la forma
se generasen producciones de acuerdo con la regla 3 entonces no se generará ninguna con la regla 2. Similarmente, si se generase una con la 5, no se generarará ninguna con la 4.
De aquí resulta que cualquier lenguaje reconocido por una autómata de pila determinista ha de ser generado por una gramática libre de contexto cuyas producciones son de la forma
