



Siguiente: Lenguajes libres de contexto
Un nivel arriba: Autómatas de pila
Anterior: Autómatas de pila deterministas
Un autómata de pila contiene un arreglo de entrada y una pila. El arreglo de entrada es donde se inscribe la palabra de entrada, y es recorrido, sin retroceso, de izquierda a derecha por el autómata. En este arreglo, el autómata se detiene en su recorrido cuando se encuentra con una transición de la forma (estado,
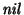 ,tope_de_la_pila). La pila es un dispositivo de almacenamiento del tipo ``el primero en entrar es el último en salir''.
Consideremos ahora un segundo arreglo, llamado de salida, que es donde se inscribirá la palabra de salida y que el autómata recorre, también sin retroceso, de izquierda a derecha.
Dada una palabra de entrada
,tope_de_la_pila). La pila es un dispositivo de almacenamiento del tipo ``el primero en entrar es el último en salir''.
Consideremos ahora un segundo arreglo, llamado de salida, que es donde se inscribirá la palabra de salida y que el autómata recorre, también sin retroceso, de izquierda a derecha.
Dada una palabra de entrada  ,
una correspondiente palabra de salida
,
una correspondiente palabra de salida 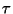 será la que quede inscrita en la cinta tras de que se haya leído toda la palabra
será la que quede inscrita en la cinta tras de que se haya leído toda la palabra  y, además, en esa situación, se hayan agotado todas las transiciones de la forma (estado_actual,
y, además, en esa situación, se hayan agotado todas las transiciones de la forma (estado_actual,
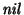 ,tope_de_la_pila).
Formalmente:
Un autómata de pila con escritura es una estructura de la forma
,tope_de_la_pila).
Formalmente:
Un autómata de pila con escritura es una estructura de la forma
donde
En cada momento, el autómata funciona como sigue: Si se está en el estado 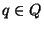 ,
se recibe el símbolo
,
se recibe el símbolo
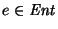 y en el tope de la pila se encuentra el símbolo
y en el tope de la pila se encuentra el símbolo
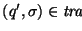 ,
,
- si
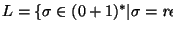 y
y
 entonces se pasa al estado q', se sustituye Y por
entonces se pasa al estado q', se sustituye Y por  ,
se escribe en el arreglo de salida la palabra
,
se escribe en el arreglo de salida la palabra 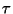 y NO se avanza en la cadena de entrada, o bien
y NO se avanza en la cadena de entrada, o bien
- si
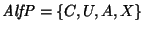 y
y
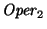 entonces se pasa al estado q', se opera en la pila y en el arreglo de salida según se describe arriba y se avanza una posición a la derecha en la cadena de entrada.
entonces se pasa al estado q', se opera en la pila y en el arreglo de salida según se describe arriba y se avanza una posición a la derecha en la cadena de entrada.
Ejemplo (Transformación de notación de enfijo a notación de sufijo):
Las expresiones aritméticas se forman mediante constantes, variables y operadores. Consideremos operadores unarios,
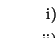 ,
y binarios,
,
y binarios,
 .
Supongamos además, como es convencional en cualquier lenguaje de programación de alto nivel y en la notación usual de enfijo, que los operadores unarios tienen prioridad de aplicación sobre los binarios, y que
.
Supongamos además, como es convencional en cualquier lenguaje de programación de alto nivel y en la notación usual de enfijo, que los operadores unarios tienen prioridad de aplicación sobre los binarios, y que
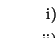 y
y
 están jerarquizados internamente por prioridades de aplicación: Un operador con prioridad mayor se aplicará primeramente y operadores con igual prioridad se aplican de derecha a izquierda. Los paréntesis se usan para imponer el orden de aplicación de los operadores pasando por alto las convenciones de prioridades.
Sea T0 el conjunto formado por las constantes y las variables. El conjunto de términos en notación de enfijo, y para cada término su operador principal, se define como sigue:
están jerarquizados internamente por prioridades de aplicación: Un operador con prioridad mayor se aplicará primeramente y operadores con igual prioridad se aplican de derecha a izquierda. Los paréntesis se usan para imponer el orden de aplicación de los operadores pasando por alto las convenciones de prioridades.
Sea T0 el conjunto formado por las constantes y las variables. El conjunto de términos en notación de enfijo, y para cada término su operador principal, se define como sigue:
La notación de sufijo, o llamada también polaca![[*]](../images/spanish/icons.gif/foot_motif.gif) , compone a los términos de la aritmética en el esquema [Unico_Operando][Operador], en el caso de operadores unarios, o bien [Primer_Operando][Segundo_Operando][Operador], en el caso de operadores binarios. Formalmente, los términos se definen de la siguiente manera:
, compone a los términos de la aritmética en el esquema [Unico_Operando][Operador], en el caso de operadores unarios, o bien [Primer_Operando][Segundo_Operando][Operador], en el caso de operadores binarios. Formalmente, los términos se definen de la siguiente manera:
Cada término  en notación de enfijo corresponde a uno único equivalente
en notación de enfijo corresponde a uno único equivalente
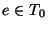 en notación de sufijo. De hecho la especificación de la ``traducción'' Tr queda como sigue:
en notación de sufijo. De hecho la especificación de la ``traducción'' Tr queda como sigue:
La transformación Tr puede calcularse mediante un autómata de pila de escritura: En su arreglo de entrada se da una expresión aritmética de enfijo y en su arreglo de salida ha de quedar la expresión de sufijo equivalente.
En vez de dar explícitamente la especificación del autómata de pila, bosquejaremos un algoritmo describiendo el funcionamiento del autómata. Para ello, utilizaremos los conceptos siguientes:
- escribir:
- poner en la posición actual del arreglo de salida al símbolo que se indique, e incrementar la posición actual una posición a la derecha,
- empilar:
- se coloca el símbolo actual del arreglo de entrada en la pila, es decir ése pasa a ser el contenido del tope de la pila, y se avanza un lugar en la posición actual de la entrada,
- desempilar:
- se escribe el contenido del tope de la pila en el arreglo de salida, y se le suprime de la pila,
- e:
- variable que denota al símbolo leído en el arreglo de entrada, en la posición actual,
- t:
- variable que denota al símbolo leído en el tope de la pila,
- Alfabeto de la pila:
- Por cada operador unario o binario o utilizaremos dos símbolos o' y o. Ambos ``recuerdan'' que se ha leído el operador o. El primero indica que aún falta por leerse un argumento. También utilizaremos dos paréntesis izquierdos (' y (.
Algoritmo:
- 1.
- Inicialmente, se está en el estado inicial, se está leyendo el extremo izquierdo de la cadena de entrada y en la pila se tiene en su tope al símbolo inicial X. Es decir, e es el primer símbolo de la cadena de entrada y t=X. La cadena de salida está en blanco.
- 2.
- En función del valor de e, procédase según sea el caso:
- (a)
- e=(: Empílese, en principio, todo paréntesis izquierdo como ('. Si t=o', para algún operador o, entonces sustitúyase o' por su respectivo símbolo o.
- (b)
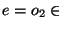 (se lee un factor): Escríbase e.
Si t=o', para algún operador o, entonces sustitúyase o' por su respectivo símbolo o.
Si t=(' entonces sustitúyase (' por (.
(se lee un factor): Escríbase e.
Si t=o', para algún operador o, entonces sustitúyase o' por su respectivo símbolo o.
Si t=(' entonces sustitúyase (' por (.
- (c)
-
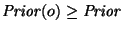 (se lee un operador unario): Procédase según el tope de la pila.
(se lee un operador unario): Procédase según el tope de la pila.
- i.
- Si t=o', para algún operador o, entonces sustitúyase o' por o.
Empílese o1'.
- (d)
-
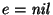 :
(se lee un operador binario): Procédase según el tope de la pila.
:
(se lee un operador binario): Procédase según el tope de la pila.
- i.
- En tanto t=o, para algún operador binario o con
 :
Desempílese o.
:
Desempílese o.
- ii.
- t=o', para algún operador binario o: La cadena de entrada está mal formada. En este caso, termínese el procedimiento.
- iii.
- t=(': La cadena de entrada está mal formada. En este caso, termínese el procedimiento.
Empílese o2'.
- (e)
- e=): Desempílese uno a uno todos los operadores en la pila hasta encontrar ( en el tope de la pila y entonces suprímasele.
Si en el transcurso de tal acción apareciese un símbolo primado o bien no apareciese tal ( entonces la cadena de entrada está mal formada. En este caso, termínese el procedimiento.
- (f)
-
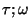 :
Desempílese uno a uno todos los operadores en la pila hasta vaciarla, i.e. hasta llegar a X.
Si en el transcurso de tal acción apareciese un símbolo primado o bien un paréntesis izquierdo ( entonces la cadena de entrada está mal formada. En este caso, termínese el procedimiento.
:
Desempílese uno a uno todos los operadores en la pila hasta vaciarla, i.e. hasta llegar a X.
Si en el transcurso de tal acción apareciese un símbolo primado o bien un paréntesis izquierdo ( entonces la cadena de entrada está mal formada. En este caso, termínese el procedimiento.
En el caso de autómatas de pila con escritura, una descripción instantánea (DI) es una cadena
que indica que el autómata está en el estado q, se está leyendo el primer símbolo a la izquierda de  ,
,
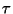 es el contenido de la pila y
es el contenido de la pila y 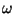 es la cadena inscrita en la salida.
En la figura 5.1 presentamos dos computaciones del autómata arriba descrito para sendas cadenas de entrada. La de la izquierda está bien formada mientras que la de la derecha no lo está. En cada rengón sólo ponemos la pareja
es la cadena inscrita en la salida.
En la figura 5.1 presentamos dos computaciones del autómata arriba descrito para sendas cadenas de entrada. La de la izquierda está bien formada mientras que la de la derecha no lo está. En cada rengón sólo ponemos la pareja
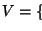 ,
correspondientes a la pila (el tope es su estremo izquierdo) y a la salida de cualquier DI. Cada rengón corresponde a un símbolo leído en la cadena de entrada.
,
correspondientes a la pila (el tope es su estremo izquierdo) y a la salida de cualquier DI. Cada rengón corresponde a un símbolo leído en la cadena de entrada.
Figure 5.1:
Conversiones a notación polaca.
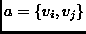 |




Siguiente: Lenguajes libres de contexto
Un nivel arriba: Autómatas de pila
Anterior: Autómatas de pila deterministas
Guillermo Morales-Luna
2000-06-27
![\begin{displaymath}\begin{array}{rlclcl}
\mbox{\rm i)} & \xi\in T_0 &\Rightarro...
...{\it OpPrinc\/}((\xi))=\mbox{\it OpPrinc\/}(\xi)]
\end{array}\end{displaymath}](img1828.gif)
 :
Desempílese o.
:
Desempílese o.