



Siguiente: Arboles y gramáticas
Un nivel arriba: Arboles de derivación
Anterior: Arboles de derivación
Recordamos que una gráfica G=(V,A) consta de un conjunto de vértices
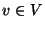 y de un conjunto de aristas A donde cada arista es una pareja de vértices. Para una arista
y de un conjunto de aristas A donde cada arista es una pareja de vértices. Para una arista
 se dice que la arista incide en sus extremos vi,vj y que éstos son adyacentes. Para cada vértice
se dice que la arista incide en sus extremos vi,vj y que éstos son adyacentes. Para cada vértice 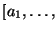 ,
el grado o la valencia de v es el número de vértices que le son adyacentes:
,
el grado o la valencia de v es el número de vértices que le son adyacentes:
Un camino entre dos vértices u,v es una sucesión de aristas
![$[a_1,\ldots, a_k]$](img1846.gif) tal que u es un extremo de a1, v lo es de ak y cualesquiera dos aristas contiguas tienen un extremo común.
Una gráfica dirigida es una gráfica tal que cada arista es un elemento del producto cartesiano
tal que u es un extremo de a1, v lo es de ak y cualesquiera dos aristas contiguas tienen un extremo común.
Una gráfica dirigida es una gráfica tal que cada arista es un elemento del producto cartesiano 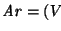 ,
es decir, cada arista posee un inicio y un fin. En tal caso, las valencias externa e interna cuentan, respectivamente, las aristas que salen de y las que entran a ese vértice, es decir, para cualquier
,
es decir, cada arista posee un inicio y un fin. En tal caso, las valencias externa e interna cuentan, respectivamente, las aristas que salen de y las que entran a ese vértice, es decir, para cualquier 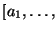 :
:
Un árbol es una gráfica dirigida
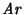 tal que
tal que
- Existe un único vértice
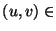 de grado interior cero. Ese vértice se dice ser la raiz de
de grado interior cero. Ese vértice se dice ser la raiz de
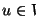 .
.
- Cualquier vértice que no es raiza posee un grado interior igual a 1.
Un vértice 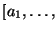 es interior si su grado exterior es mayor que 0. Los vértices que no son interiores son hojas. Si
es interior si su grado exterior es mayor que 0. Los vértices que no son interiores son hojas. Si
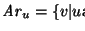 entonces v se dice ser un hijo de u y u el padre de v. Dos vértices con un mismo padre se dicen ser hermanos.
entonces v se dice ser un hijo de u y u el padre de v. Dos vértices con un mismo padre se dicen ser hermanos.
Observación 1.1
- 1.
- Cada vértice
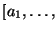 tiene un camino único que lo conecta con la raiz. El número de aristas en ese camino es la altura del vértice. Los vértices visitados por ese camino son los ancestros de v.
tiene un camino único que lo conecta con la raiz. El número de aristas en ese camino es la altura del vértice. Los vértices visitados por ese camino son los ancestros de v.
- 2.
- Para cada vértice
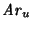 el conjunto
el conjunto
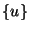 adquiere naturalmente una estructura de árbol. Se dice ser el subárbol enraizado en u.
adquiere naturalmente una estructura de árbol. Se dice ser el subárbol enraizado en u.
- 3.
- En cada vértice
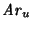 el subárbol
el subárbol
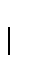 es la unión de
es la unión de 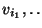 junto con los subárboles enraizados en los hijos de u.
junto con los subárboles enraizados en los hijos de u.
Todo árbol tiene una estructura de conjunto ordenado mediante el orden
Sin embargo, el árbol se dice ordenado sólo si en cada vértice interior el conjunto de sus hijos posee un orden lineal, es decir, a los hijos
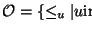 de todo vértice u se los puede ordenar de menor a mayor. Denotemos por
de todo vértice u se los puede ordenar de menor a mayor. Denotemos por 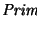 al orden de los hijos de u.
Para cada familia
al orden de los hijos de u.
Para cada familia
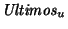 de órdenes en hijos de vértices interiores se puede definir, por ejemplo, los órdenes siguientes en el árbol Ar:
de órdenes en hijos de vértices interiores se puede definir, por ejemplo, los órdenes siguientes en el árbol Ar:
- Preorden:
- Cada padre precede a sus hermanos mayores y a los vértices del que es ancestro.
- Entreorden:
- En cada vértice interior se divide al conjunto de sus hijos en dos conjuntos
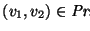 y
y
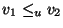 de manera que para cualquier pareja
de manera que para cualquier pareja
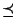 se cumpla
se cumpla
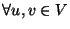 .
En el entreorden se tiene que cada padre precede a sus hermanos mayores y a sus últimos hijos, pero sucede a sus hijos primeros.
.
En el entreorden se tiene que cada padre precede a sus hermanos mayores y a sus últimos hijos, pero sucede a sus hijos primeros.
- Postorden:
- Cada padre sucede a sus hermanos menores y a los vértices del que es ancestro.
Cualquiera de estos órdenes es un orden de izquierda a derecha: 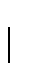 es un orden de izquierda a derecha si cualesquiera dos vértices con subárboles ajenos son tales que todos los vértices en el subárbol de uno anteceden a cualquier vértice en el subárbol del otro, i. e.
es un orden de izquierda a derecha si cualesquiera dos vértices con subárboles ajenos son tales que todos los vértices en el subárbol de uno anteceden a cualquier vértice en el subárbol del otro, i. e.
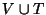 :
:
Todo orden de izquierda a derecha es total: cualesquiera dos vértices en el árbol son comparables.
En un tal orden, la hoja mínima se dice ser la hoja siniestra (leftmost) y la máxima es la hoja diestra (rightmost).




Siguiente: Arboles y gramáticas
Un nivel arriba: Arboles de derivación
Anterior: Arboles de derivación
Guillermo Morales-Luna
2000-06-27
 se dice que la arista incide en sus extremos vi,vj y que éstos son adyacentes. Para cada vértice
se dice que la arista incide en sus extremos vi,vj y que éstos son adyacentes. Para cada vértice ![$[a_1,\ldots, a_k]$](img1846.gif) tal que u es un extremo de a1, v lo es de ak y cualesquiera dos aristas contiguas tienen un extremo común.
Una gráfica dirigida es una gráfica tal que cada arista es un elemento del producto cartesiano
tal que u es un extremo de a1, v lo es de ak y cualesquiera dos aristas contiguas tienen un extremo común.
Una gráfica dirigida es una gráfica tal que cada arista es un elemento del producto cartesiano  es la unión de
es la unión de