



Siguiente: Transformaciones equivalentes de gramáticas
Un nivel arriba: Arboles de derivación
Anterior: Gráficas y árboles
Sea
G=(V,T,P,s0) una gramática libre de contexto.
Un árbol gramatical en G es un árbol ordenado
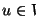 tal que
tal que
- los vértices de
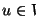 están etiquetados con etiquetas en el alfabeto de la gramática
están etiquetados con etiquetas en el alfabeto de la gramática 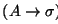 o con la etiqueta vacía,
o con la etiqueta vacía,
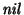 ,
y
,
y
- cada vértice interior corresponde a una producción en G, es decir, si A es la etiqueta del vértice interior v0 y
![$\sigma=[e(v)\vert v\mbox{\rm es hijo de }v_0]$](img1869.gif) es la palabra formada por las etiquetas de los hijos de v0 entonces
es la palabra formada por las etiquetas de los hijos de v0 entonces
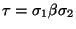 es una producción en P.
es una producción en P.
Un árbol gramatical es de derivación si su raiz está etiquetada con el símbolo inicial s0 y todas sus hojas tienen etiquetas terminales o vacía. La leyenda de un árbol de derivación es la palabra obtenida al concatenar ordenadamente, con cualquier orden de izquierda a derecha, las etiquetas de sus hojas.
Así pues, todo árbol de derivación tiene como leyenda una palabra en L(G). Recíprocamente, para cada palabra  en L(G) existe un árbol de derivación cuya leyenda coincide con
en L(G) existe un árbol de derivación cuya leyenda coincide con  .
Si
.
Si
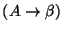 y
y
 ,
donde
,
donde
 es una producción en P y
es una producción en P y 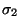 consiste únicamente de símbolos terminales, decimos que
consiste únicamente de símbolos terminales, decimos que 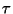 se sigue de
se sigue de  por la aplicación diestra de una producción. Una derivación es diestra si todas las aplicaciones de producciones hechas son diestras. Las derivaciones siniestras se definen simétricamente.
Ejemplo.
Consideremos las siguientes producciones:
por la aplicación diestra de una producción. Una derivación es diestra si todas las aplicaciones de producciones hechas son diestras. Las derivaciones siniestras se definen simétricamente.
Ejemplo.
Consideremos las siguientes producciones:
Sendas derivaciones siniestra y diestra de la palabra
a(ba2)2=abaabaa son las siguientes:
En el lenguaje L(G) generado por esta gramática se encuentran incluidos los siguientes lenguajes:
Para concluir esta sección presentaremos las nociones de ambigüedad en gramáticas.
Una gramática libre de contexto
G=(V,T,P,s0) se dice ser ambigua si alguna palabra de su lenguaje,
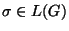 posee dos derivaciones diestras.
Ejemplos.
1. La gramática G cuyas producciones son
posee dos derivaciones diestras.
Ejemplos.
1. La gramática G cuyas producciones son
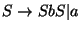 es ambigua pues la palabra (ab)2a posee dos derivaciones diestras:
es ambigua pues la palabra (ab)2a posee dos derivaciones diestras:
2. Si para la gramática
G=(V,T,P,s0) incluimos una copia V' del conjunto de variables no-iniciales más copias de las producciones de P con símbolos en S' entonces la nueva gramática
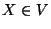 es ambigua pues cada derivación diestra puede derivarse considerando símbolos en V o en su contraparte V'.
es ambigua pues cada derivación diestra puede derivarse considerando símbolos en V o en su contraparte V'.




Siguiente: Transformaciones equivalentes de gramáticas
Un nivel arriba: Arboles de derivación
Anterior: Gráficas y árboles
Guillermo Morales-Luna
2000-06-27
 ,
donde
,
donde
 es una producción en P y
es una producción en P y  ,
donde
,
donde
 y
y