



Siguiente: Formas normales
Un nivel arriba: Transformaciones equivalentes de gramáticas
Anterior: Supresión de producciones vacías
Una producción unitaria es una de la forma
 con
con 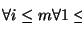 .
.
Proposición 2.3
Toda gramática libre de contexto
G=(V,T,P,S) que no genere a la palabra vacía se puede transformar en una gramática libre de contexto
G'=(V',T,P',S') sin variables inútiles ni producciones vacías ni producciones unitarias equivalente a G.
En efecto, dada una gramática G, construyamos, mediante la construcción anterior, la gramática G' equivalente a G sin variables inútiles ni producciones vacías. Si hubiese aún producciones unitarias podríamos acomodarlas todas en una lista como la siguiente:
Así pues
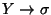 .
Pues bien, ahora para cada par de producciones
.
Pues bien, ahora para cada par de producciones
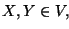 ,
,
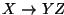 con
con
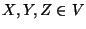 ,
a esas producciones las sustituimos por la producción
,
a esas producciones las sustituimos por la producción
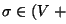 .
La gramática G' que así obtenemos es equivalente a G'', y por tanto a G, y es como la anunciada en la proposición.
.
La gramática G' que así obtenemos es equivalente a G'', y por tanto a G, y es como la anunciada en la proposición.
Guillermo Morales-Luna
2000-06-27
 con
con