



Siguiente: Supresión de símbolos inútiles
Un nivel arriba: Lenguajes libres de contexto
Anterior: Arboles y gramáticas
Recordamos que una gramática formal
G=(V,T,P,S), donde V es el conjunto de símbolos variables, T es el conjunto de símbolos terminales, P es el conjunto de producciones y S es el símbolo inicial, se dice ser libre de contexto si sus producciones son de la forma
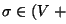 ,
con
,
con 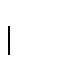 y
y
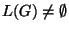 .
Veremos en esta sección que toda gramática libre de contexto puede ser convertida, algorítmicamente, a gramáticas equivalentes que no poseen variables que no se utilicen o que no contengan produccciones con consecuente vacío o cuyas producciones sean una mera sustitución de variables.
A lo largo de esta sección,
G=(V,T,P,S) denotará siempre una gramática libre de contexto.
.
Veremos en esta sección que toda gramática libre de contexto puede ser convertida, algorítmicamente, a gramáticas equivalentes que no poseen variables que no se utilicen o que no contengan produccciones con consecuente vacío o cuyas producciones sean una mera sustitución de variables.
A lo largo de esta sección,
G=(V,T,P,S) denotará siempre una gramática libre de contexto.
Guillermo Morales-Luna
2000-06-27
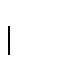 y
y