



Siguiente: Series sobre los racionales
Un nivel arriba: Series de potencias e
Anterior: Series de potencias e
Sea
G=(V,T,P,s0) una gramática libre de contexto. Para cada símbolo variable 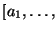 sea
sea
 el conjunto de palabras derivadas por s en G. Así pues, el lenguaje de G es, (s0)G. De hecho, para cada palabra
el conjunto de palabras derivadas por s en G. Así pues, el lenguaje de G es, (s0)G. De hecho, para cada palabra
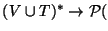 definamos
definamos
Consideremos la transformación
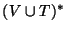 ,
,
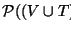 ,
del diccionario
,
del diccionario
 a la clase de lenguajes
a la clase de lenguajes
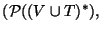 .
La operación ``suma'' de
.
La operación ``suma'' de
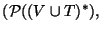 es la unión conjuntista y su producto es el obtenido ``al concatenar lenguajes''
es la unión conjuntista y su producto es el obtenido ``al concatenar lenguajes''
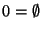 tiene una estructura de semianillo no-conmutativo, es decir,
Ahora, para
tiene una estructura de semianillo no-conmutativo, es decir,
Ahora, para
 la ``alternancia'' puede ser vista como una suma, y por tanto
la ``alternancia'' puede ser vista como una suma, y por tanto
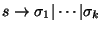 ,
y, ya que la gramática G es libre de contexto, se tiene también la identidad
,
y, ya que la gramática G es libre de contexto, se tiene también la identidad
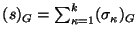 .
Así pues la transformación
.
Así pues la transformación
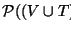 es un homomorfismo de semianillos.
Consecuentemente, toda gramática libre de contexto puede ser presentada de manera algebraica: A cada producción de la forma
es un homomorfismo de semianillos.
Consecuentemente, toda gramática libre de contexto puede ser presentada de manera algebraica: A cada producción de la forma
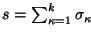 se la escribe equivalentemente como
se la escribe equivalentemente como
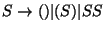 ,
o bien, dando la gramática como supuesta, simplemente como la ecuación básica
,
o bien, dando la gramática como supuesta, simplemente como la ecuación básica
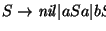 .
Ejemplos.
1. La gramática de cadenas equilibradas de paréntesis,
.
Ejemplos.
1. La gramática de cadenas equilibradas de paréntesis,
 da la ecuación básica:
S=()+(S)+SS.
da la ecuación básica:
S=()+(S)+SS.
2. La gramática de palíndromas
 da la ecuación básica:
S=1+ aSa+bSb.
da la ecuación básica:
S=1+ aSa+bSb.
3. La gramática con producciones
da las ecuaciones básicas
Mediante sustituciones sucesivas se puede generar nuevas ecuaciones a partir de ecuaciones generadas previamente:
- toda ecuación básica es generada,
- si
 es básica y
s1=G(V,T) ha sido generada entonces al sustituir s1 por G(V,T) en
es básica y
s1=G(V,T) ha sido generada entonces al sustituir s1 por G(V,T) en
 ,
,
da una nueva ecuación generada.
La serie generativa del lenguaje L(G) se obtiene al tomar al ``supremo'' de todas las ecuaciones generadas a partir de la ecuación básica que tiene como extremo izquierdo al símbolo inicial.
Como mero ejemplo, es fácil ver que para la ecuación básica
S=1+ aSa+bSb la serie generativa quedará de la forma




Siguiente: Series sobre los racionales
Un nivel arriba: Series de potencias e
Anterior: Series de potencias e
Guillermo Morales-Luna
2000-06-27
 el conjunto de palabras derivadas por s en G. Así pues, el lenguaje de G es, (s0)G. De hecho, para cada palabra
el conjunto de palabras derivadas por s en G. Así pues, el lenguaje de G es, (s0)G. De hecho, para cada palabra
 a la clase de lenguajes
a la clase de lenguajes
 ,
y
,
y
 la ``alternancia'' puede ser vista como una suma, y por tanto
la ``alternancia'' puede ser vista como una suma, y por tanto
 da la ecuación básica:
S=()+(S)+SS.
da la ecuación básica:
S=()+(S)+SS.
 da la ecuación básica:
S=1+ aSa+bSb.
da la ecuación básica:
S=1+ aSa+bSb.
 es básica y
s1=G(V,T) ha sido generada entonces al sustituir s1 por G(V,T) en
es básica y
s1=G(V,T) ha sido generada entonces al sustituir s1 por G(V,T) en
 ,
,