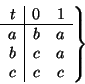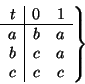Siguiente: Autómatas de pila
Un nivel arriba: Autómatas
Anterior: Autómatas
Estos son los autómatas finitos más sencillos. Se construyen a partir de un conjunto de estados Q y de un conjunto de símbolos de entrada T. Su funcionamiento queda determinado por una función de transición
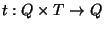 .
Si t(q,s)=p esto se interpreta como que el autómata transita del estado q al estado p cuando arriba el símbolo s.
En todo autómata finito se cuenta con un estado inicial,
.
Si t(q,s)=p esto se interpreta como que el autómata transita del estado q al estado p cuando arriba el símbolo s.
En todo autómata finito se cuenta con un estado inicial,
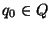 y un conjunto de estados finales
y un conjunto de estados finales
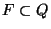 .
Con todo esto definido, la estructura
.
Con todo esto definido, la estructura
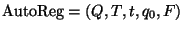 es un autómata regular.
De manera natural, t se extiende a una función de transición
es un autómata regular.
De manera natural, t se extiende a una función de transición
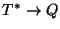 :
Toda palabra se aplica al autómata y éste, partiendo del estado inicial, transita con cada símbolo de la palabra dada según lo especifique t, correspondiendo a ese símbolo y al estado actual en el autómata. Una palabra es reconocida por el automata si lo hace arribar a un estado final. El lenguaje del autómata consta de todas las palabras reconocidas.
:
Toda palabra se aplica al autómata y éste, partiendo del estado inicial, transita con cada símbolo de la palabra dada según lo especifique t, correspondiendo a ese símbolo y al estado actual en el autómata. Una palabra es reconocida por el automata si lo hace arribar a un estado final. El lenguaje del autómata consta de todas las palabras reconocidas.
Ejemplo: Sea
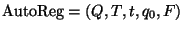 el autómata cuyo conjunto de estados es
el autómata cuyo conjunto de estados es
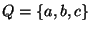 ,
el de símbolos de entrada es
,
el de símbolos de entrada es
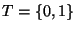 ,
su estado inicial es q0 = a y el conjunto de estados finales es
,
su estado inicial es q0 = a y el conjunto de estados finales es
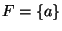 .
Su transición queda determinada por la tabla
.
Su transición queda determinada por la tabla
Observamos que, partiendo del estado a, mientras lleguen 1's se está en el estado inicial, con un 0 se pasa a b, con un segundo 0 se pasa a c y de ahí no se sale más. En b, al llegar un 1 se regresa al estado inicial. Así pues, para arribar al estado a desde a mismo la cadena de entrada ha de ser una sarta de varias de 1's separadas éstas por únicos 0's. En otras palabras, el autómata reconoce al lenguaje
(1+0)*1+.




Siguiente: Autómatas de pila
Un nivel arriba: Autómatas
Anterior: Autómatas
Guillermo Morales-Luna
2000-06-27