Siguiente: Autómatas lineales
Un nivel arriba: Autómatas
Anterior: Autómatas regulares
Estos autómatas finitos cuentan con un dispositivo de memoria muy elemental, del tipo pila, el cual es un almacenamiento lineal que funciona bajo el principio PEUS![[*]](../images/spanish/icons.gif/foot_motif.gif) : Primero en Entrar, Ultimo en Salir.
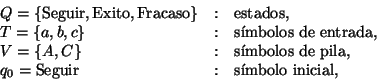
Sea Q un conjunto de estados, sea T el alfabeto de entrada y sea V un alfabeto de pila. La función de transición es de la forma
: Primero en Entrar, Ultimo en Salir.
Sea Q un conjunto de estados, sea T el alfabeto de entrada y sea V un alfabeto de pila. La función de transición es de la forma
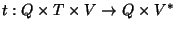 ,
donde la relación
,
donde la relación
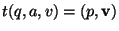 se interpreta como sigue: ``Si se está en el estado q, arriba el símbolo a y en el tope de la pila está el símbolo b entonces se pasa al estado p y se empila la palabra
se interpreta como sigue: ``Si se está en el estado q, arriba el símbolo a y en el tope de la pila está el símbolo b entonces se pasa al estado p y se empila la palabra
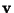 ''.
Un autómata de pila reconoce a una palabra si, tras haberla leído, termina con su pila vacía.
''.
Un autómata de pila reconoce a una palabra si, tras haberla leído, termina con su pila vacía.
Ejemplo: Las cadenas equilibradas de paréntesis son reconocidas por un autómata de pila determinista. Recordamos que
- 1.
- () es una cadena equilibrada de paréntesis, (CEP).
- 2.
- Si
 es una CEP entonces
es una CEP entonces 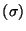 es una CEP.
es una CEP.
- 3.
- La concatenación de dos CEP's es una CEP.
Para describir a un autómata que reconozca CEP's, representemos al paréntesis que abre ``('' con el símbolo a, al paréntesis que cierra ``)'' con c, y con b al ``blanco'', es decir, al fin de la cadena de entrada.
Consideremos el autómata de pila cuyas componentes son las siguientes:
y cuya función de transición actúa como sigue,
Es claro que este autómata de pila reconoce al lenguaje CEP.




Siguiente: Autómatas lineales
Un nivel arriba: Autómatas
Anterior: Autómatas regulares
Guillermo Morales-Luna
2000-06-27