



Siguiente: Autómatas de pila no-deterministas
Un nivel arriba: Autómatas
Anterior: Autómatas de pila
Los autómatas lineales son autómatas de pila deterministas que a lo largo de su computación sólo hacen un ``cambio de turno''. A grandes rasgos, esto significa que toda computación consiste de un procedimiento de empilar consecutivamente para después pasar a desempilar.
Ejemplo: Consideremos el lenguaje de palíndromas con una marca central:
Consideremos el autómata de pila cuyas componentes son las siguientes:
y cuya función de transición actúa como sigue,
donde 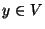 y b es el símbolo ``blanco''. En cualquier otra instancia de t, ésta transitará al estado de fracaso.
Es claro que este autómata de pila reconoce al lenguaje L.
y b es el símbolo ``blanco''. En cualquier otra instancia de t, ésta transitará al estado de fracaso.
Es claro que este autómata de pila reconoce al lenguaje L.
Guillermo Morales-Luna
2000-06-27

