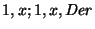 |
: |
con cualquier cosa, salvo ``)'', aváncese a la derecha,
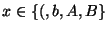 , , |
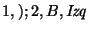 |
: |
con el primer ``)'', márquese y retrocédase, |
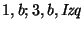 |
: |
si la lista se acaba, revísese que todo haya sido marcado, |
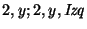 |
: |
con cualquier cosa, salvo ``('', continúese el retroceso,
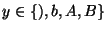 , , |
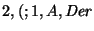 |
: |
márquese el ``('' que empata y repítase el ciclo, |
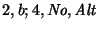 |
: |
se termina la cadena y no existe el correspondiente ``(''. No hay equilibrio. |
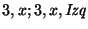 |
: |
retrocédase ignorando las marcas,
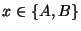 , , |
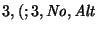 |
: |
si quedare un ``('', éste ya no podría empatarse. No hay equilibrio. |
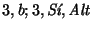 |
: |
se agotó la cadena y todo se marcó. Sí hay equilibrio. |
|

