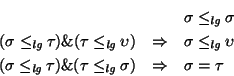Proposición 2.7
El orden lexicográfico satisface las propiedades siguientes:
- 1.
- Es, en efecto, un orden, es decir, cualesquiera que sean las palabras
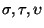 ,
,
- 2.
- Es lineal, es decir,
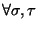 :
:
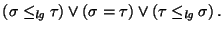
- 3.
- Es congruente por la izquierda, es decir,
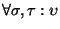 ,
,
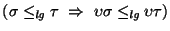 .
Mas no lo es por la derecha.
.
Mas no lo es por la derecha.