



Siguiente: Parejas de igual longitud
Un nivel arriba: Ejemplos de gramáticas
Anterior: Proposiciones bien formadas
Sea
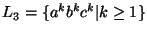 el lenguaje que consta de tres bloques consecutivos de a's, b's y c's de iguales longitudes. Construiremos una gramática para generar este lenguaje.
Consideremos las producciones siguientes:
el lenguaje que consta de tres bloques consecutivos de a's, b's y c's de iguales longitudes. Construiremos una gramática para generar este lenguaje.
Consideremos las producciones siguientes:
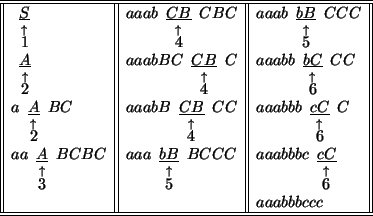
En la tabla (2.2) vemos, a manera de ejemplo, la generación de la palabra
a3b3c3=aaabbbccc.
Table 2.2:
Un ejemplo para la gramática de L3.
 |
Con la gramática descrita, tenemos, efectivamente, que
- i)
- toda palabra generada en ella tiene una longitud múltiplo de 3, y
- ii)
- toda palabra generada es de la forma akbkck para algún
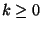 .
.
Así pues, el lenguaje generado por la gramática es
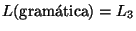 .
.
Guillermo Morales-Luna
2000-06-27

