Siguiente: Tipos de gramáticas
Un nivel arriba: Equivalencia de gramáticas
Anterior: Equivalencia de gramáticas
Palíndromas
Sea
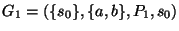 la gramática con producciones
la gramática con producciones
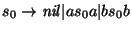 Observamos que con la aplicación de cada regla,
Observamos que con la aplicación de cada regla,
se añade un par de símbolos, aquí iguales, o bien no se añade símbolo alguno, y el símbolo que se añade al inicio se ha de ``equilibrar'' con otro igual al final.
Así pues, es muy fácil ver que el lenguaje generado por esta gramática consta de los palíndromas de longitud par sobre (a+b),
Sea G2 la gramática que coincide con G1 salvo en que contiene además las producciones
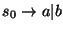 .
Entonces G2 genera a todos los palíndromas en (a+b)*. G2 subsume a la gramática G1.
.
Entonces G2 genera a todos los palíndromas en (a+b)*. G2 subsume a la gramática G1.
Cadenas equilibradas de paréntesis
Recordamos que las cadenas equilibradas de paréntesis (CEP) quedan caracterizadas por las siguientes proposiciones:
a) () es una CEP.
b) Si E,F son dos CEP's entonces tanto (E) como EF son CEP's.
c) Las CEP's son únicamente las cadenas obtenidas por las reglas anteriores.
Así pues consideremos la gramática
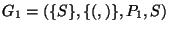 ,
donde P1 consta de las reglas
,
donde P1 consta de las reglas
De acuerdo con las reglas descritas arriba, G1 genera a las CEP's.
Por ejemplo, una derivación de la cadena ()(()()) se muestra en la tabla (2.8-(a)).
Table 2.8:
Ejemplo de una CEP generada en sendas gramáticas equivalentes. (Se indica con una flecha sobre cuál símbolo variable se aplica la regla indicada por el número de abajo.)
 |
Consideremos ahora la gramática G2 con símbolo inicial S y producciones
Esta gramática también genera a las cadenas equilibradas de paréntesis. Tan solo como un ejemplo, se muestra la derivación de la cadena anterior en la tabla (2.8-(b)).
Para ver que G1 subsume a G2, es decir, que toda palabra terminal generada en G2 es generada también en G1, basta observar que para cualquier
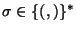 :
:
De hecho, estas relaciones pueden ser demostradas simultáneamente por inducción en el número de reglas aplicadas en G2 para obtener la palabra  .
En efecto, supongamos que la relación ii) es verdadera. Entonces la i) también lo es, tan solo por la aplicación de la regla s). Ahora, si
.
En efecto, supongamos que la relación ii) es verdadera. Entonces la i) también lo es, tan solo por la aplicación de la regla s). Ahora, si  se obtiene de A mediante una sola regla, esta regla ha de ser la a.1) y en este caso ii) se cumple. Si
se obtiene de A mediante una sola regla, esta regla ha de ser la a.1) y en este caso ii) se cumple. Si  se obtiene de n+1 reglas entonces la primera regla ha de ser cualquiera de
a.2),a.3),a.4) las cuales son congruentes con la hipótesis ii).
Ahora, para ver que G2 subsume a G1 hay que ver que toda cadena generada en G1 es generada también en G2. Para esto se procede también por inducción en el número de reglas aplicadas para generar una palabra terminal
se obtiene de n+1 reglas entonces la primera regla ha de ser cualquiera de
a.2),a.3),a.4) las cuales son congruentes con la hipótesis ii).
Ahora, para ver que G2 subsume a G1 hay que ver que toda cadena generada en G1 es generada también en G2. Para esto se procede también por inducción en el número de reglas aplicadas para generar una palabra terminal  .
Si
.
Si  se obtiene mediante una sola regla en G1, entonces esa regla ha de ser la 1. y
se obtiene mediante una sola regla en G1, entonces esa regla ha de ser la 1. y 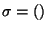 .
Una derivación de ella en G2 es
.
Una derivación de ella en G2 es
Ahora, supongamos que  se obtiene mediante la aplicación de n+1 reglas en G1.
Supongamos que la primera es de la forma 2.:
se obtiene mediante la aplicación de n+1 reglas en G1.
Supongamos que la primera es de la forma 2.:
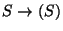 .
Entonces
.
Entonces
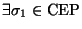 tal que
tal que
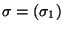 y
y 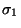 se deriva con a lo sumo n aplicaciones de reglas en G1. Por inducción, tenemos que
se deriva con a lo sumo n aplicaciones de reglas en G1. Por inducción, tenemos que 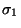 se deriva en G2 y por la relación ii) tendremos
se deriva en G2 y por la relación ii) tendremos
![$G_2\vdash[A\stackrel{*}{\rightarrow} \sigma_1)]$](img482.gif) ,
de hecho,
,
de hecho,
![$G_2\vdash[A\stackrel{*}{\rightarrow} \sigma_1A]$](img483.gif) .
Así pues, una derivación de
.
Así pues, una derivación de  en G2 es
en G2 es
Si la primera regla aplicada es 3.:
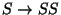 ,
entonces se construye de manera análoga una derivación en G2.
Así pues, las dos gramáticas dadas son equivalentes.
,
entonces se construye de manera análoga una derivación en G2.
Así pues, las dos gramáticas dadas son equivalentes.




Siguiente: Tipos de gramáticas
Un nivel arriba: Equivalencia de gramáticas
Anterior: Equivalencia de gramáticas
Guillermo Morales-Luna
2000-06-27