Lema 2.2
Sea
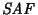
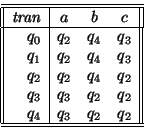
un semiautómata finito. Entonces su monoide
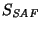
puede ser dotado de una estructura de semiautómata, y si
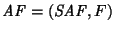
es un autómata cuyo semiatautómata adyacente es SAF, entonces puede distinguirse a algunas clases de equivalencia de manera que el autómata resultante queda subsumido por
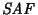
.
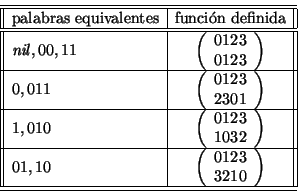
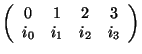 denotamos a la función
denotamos a la función
![\begin{displaymath}\begin{array}{\vert\vert r\vert llll\vert\vert}\hline\hline
...
...1]} & {[0]} & {[\mbox{\it nil\/}]} \\ \hline\hline
\end{array}\end{displaymath}](img848.gif)
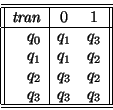
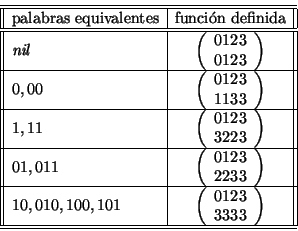
![\begin{displaymath}\begin{array}{\vert\vert r\vert lllll\vert\vert}\hline\hline ...
... {[10]} & {[10]} & {[10]} & {[10]} \\ \hline\hline
\end{array}\end{displaymath}](img851.gif)

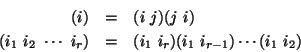
![\begin{eqnarray*}\mbox{\it tran\/}_S:S_{\mbox{\scriptsize\it SAF}}\times \mbox{\...
...\sigma],e) &\mapsto& \mbox{\it tran\/}_S([\sigma],e)=[\sigma e]
\end{eqnarray*}](img883.gif)
![\begin{eqnarray*}h:S_{\mbox{\scriptsize\it AF}} &\rightarrow& \mbox{\it AF\/} \\...
...&\mapsto& h([\sigma])=T(\sigma)=\mbox{\it tran\/}^*(q_0,\sigma)
\end{eqnarray*}](img887.gif)
![\begin{eqnarray*}h_m:S_{\mbox{\scriptsize\it AF}_1} &\rightarrow& S_{\mbox{\scri...
...ox{\scriptsize\it AF}_1})=[\sigma]_{\mbox{\scriptsize\it AF}_2}
\end{eqnarray*}](img890.gif)
![\begin{eqnarray*}{[\sigma_1]_{\mbox{\scriptsize\it AF}_1}=[\sigma_2]_{\mbox{\scr...
...{\scriptsize\it AF}_2}=[\sigma_2]_{\mbox{\scriptsize\it AF}_2},
\end{eqnarray*}](img891.gif)