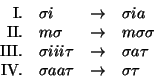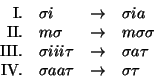Siguiente: KENNINGS: Poesía antigua islandesa
Un nivel arriba: Reglas de transformación
Anterior: Reglas de transformación
Este ejemplo aparece en el capítulo 1 del libro de Hofstadter ([15]).
Consideremos las reglas siguientes:
Los caracteres griegos representan a palabras en el alfabeto
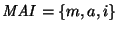 .
La primera regla dice que a toda palabra que termina con i puede añadírsele una a, la segunda, que toda palabra que comience con m puede repetir su ``resto'', la tercera, que cualquier cadena de tres i-es consecutivas puede cambiarse por una a, y, finalmante, que cualesquiera dos a-es consecutivas pueden ser suprimidas.
Como ejemplos de derivaciones están los mostrados en la figura (3).
.
La primera regla dice que a toda palabra que termina con i puede añadírsele una a, la segunda, que toda palabra que comience con m puede repetir su ``resto'', la tercera, que cualquier cadena de tres i-es consecutivas puede cambiarse por una a, y, finalmante, que cualesquiera dos a-es consecutivas pueden ser suprimidas.
Como ejemplos de derivaciones están los mostrados en la figura (3).
Figure 3:
Derivaciones en el sistema MAI.
 |
Para cada palabra  sea
sea
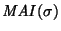 el conjunto de palabras en el alfabeto MAI que pueden ser derivadas a partir de la palabra
el conjunto de palabras en el alfabeto MAI que pueden ser derivadas a partir de la palabra  mediante una sucesión finita de aplicaciones de las reglas de transformación. Naturalmente, surgen los problemas siguientes:
mediante una sucesión finita de aplicaciones de las reglas de transformación. Naturalmente, surgen los problemas siguientes:
- Problema de la palabra.
- Dadas dos palabras
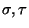 decidir si acaso
decidir si acaso
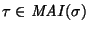 ,
es decir, decidir si acaso una palabra es o no derivable desde alguna otra.
,
es decir, decidir si acaso una palabra es o no derivable desde alguna otra.
- Problema de equivalencia.
- Dadas dos palabras
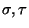 decidir si acaso
decidir si acaso
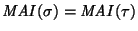 ,
es decir, decidir si acaso cualquier palabra es derivable desde una de las dos palabras si y sólo si es derivable desde la otra.
,
es decir, decidir si acaso cualquier palabra es derivable desde una de las dos palabras si y sólo si es derivable desde la otra.
- Problema de derivación óptima.
- Dadas dos palabras
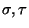 tales que
tales que
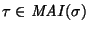 ,
localizar la sucesión de transformaciones más corta que transforma a
,
localizar la sucesión de transformaciones más corta que transforma a  en
en 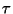 .
.




Siguiente: KENNINGS: Poesía antigua islandesa
Un nivel arriba: Reglas de transformación
Anterior: Reglas de transformación
Guillermo Morales-Luna
2000-06-27