


Siguiente: Expresiones regulares y sistemas
Un nivel arriba: Expresiones regulares
Anterior: Matrices de expresiones regulares
Veremos en esta sección que se cumple el recíproco de la proposición 4.2.3: Todo lenguaje regular ha de ser formalmente regular.
Sea
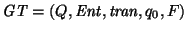 una gráfica de transición. Consideremos la siguiente transformación:
una gráfica de transición. Consideremos la siguiente transformación:
Observación 4.1
El lenguaje de la gráfica de transición

coincide con el conjunto
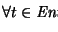
.
Por tanto, se tiene la igualdad conjuntista
donde
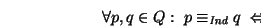 .
Y puesta la igualdad anterior como una expresión regular queda
.
Y puesta la igualdad anterior como una expresión regular queda
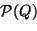 |
(39) |
Ahora, de manera similar a como se hizo en la ec. (3.6), definimos la relación de indistinguibilidad entre los estados de GT haciendo
![\begin{displaymath}\forall p,q\in Q:\ p\equiv_{\mbox{\scriptsize\it Ind}}q\ \Lef...
...arrow \mbox{\it tran\/}^*(q,\tau)\cap F\not=\emptyset\right]
\end{displaymath}](img1396.gif) |
(40) |
y de hecho la extendemos al conjunto de subconjuntos de estados,
 ,
haciendo
,
haciendo
 |
(41) |
Y, también a como se hizo en el caso de los autómatas finitos, se tiene inducida una relación de indistinguibilidad en el diccionario de entrada:
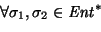 |
(42) |
donde
 .
.
Ahora bien, se tiene una correspondencia entre la imagen de 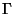 ,
o sea el conjunto de estados de
,
o sea el conjunto de estados de
 ,
y las partes de Q que son accesibles desde el estado inicial q0 en la gráfica.
Por tanto, podemos calcular al autómata cociente
,
y las partes de Q que son accesibles desde el estado inicial q0 en la gráfica.
Por tanto, podemos calcular al autómata cociente
 de manera similar a como se calcula el autómata equivalente a una gráfica de transición. En la Figura 4.1 presentamos el seudocódigo de este procedimiento.
Si
de manera similar a como se calcula el autómata equivalente a una gráfica de transición. En la Figura 4.1 presentamos el seudocódigo de este procedimiento.
Si
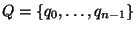 es el conjunto de estados de la gráfica, la lista
es el conjunto de estados de la gráfica, la lista
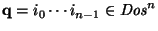 denota al subconjunto Q' tal que para todo j,
denota al subconjunto Q' tal que para todo j,
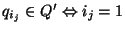 .
.
Figure:
Cálculo de la imagen de 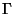 para una gráfica de transición dada.
para una gráfica de transición dada.
|
|
Habiendo calculado
 ,
supongamos que
,
supongamos que
donde
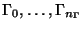 corresponde a la palabra vacía.
En este caso, las ecuaciones 4.28 dan un sistema de
corresponde a la palabra vacía.
En este caso, las ecuaciones 4.28 dan un sistema de
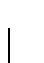 ecuaciones con
ecuaciones con
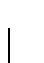 ``incógnitas''
``incógnitas''
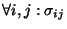 de la forma
de la forma
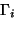 |
(43) |
donde
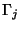 es la suma de símbolos que en
es la suma de símbolos que en
 hacen transitar a
hacen transitar a 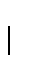 hacia
hacia 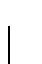 :
:
y
Puesto de manera matricial, el sistema de ecuaciones 4.32 queda de la forma
y por la manera en la que se construyó, la matriz
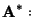 no posee la CPV, por tanto
no posee la CPV, por tanto
En la primera entrada de este vector, es decir, la correspondiente a 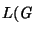 ,
se obtiene una expresión regular que describe al lenguaje reconocido por la gráfica de transición.
En resumen, se tiene la
,
se obtiene una expresión regular que describe al lenguaje reconocido por la gráfica de transición.
En resumen, se tiene la
Proposición 4.1 (Kleene)
El lenguaje reconocido por cualquier gráfica de transición se puede expresar mediante una expresión regular. Es decir, todo lenguaje regular es formalmente regular.
Así pues, para una gráfica de transición
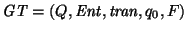 con sólo dos estados q1 y q2. Hagamos
con sólo dos estados q1 y q2. Hagamos
Entonces, de la ec. (4.27) obtenemos:
![$L(\mbox{\it GT\/})=\left[a_{11}^* a_{12} a_{22}^* a_{21}\right]^* a_{11}^*b_1+a_{12} a_{22}^*b_2.$](img1431.gif)
Ejemplo:
Sea
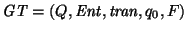 la gráfica de transición vista anteriormente, donde
la gráfica de transición vista anteriormente, donde
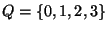 ,
,
 ,
q0=0,
,
q0=0, 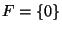 y las transiciones son
y las transiciones son
 .
Al aplicar el algoritmo 4.1 obtenemos la tabla siguiente:
.
Al aplicar el algoritmo 4.1 obtenemos la tabla siguiente:
Por tanto,
y se obtiene el sistema de ecuaciones
Puesto de manera matricial el anterior sistema de ecuaciones queda de la forma![[*]](../images/spanish/icons.gif/foot_motif.gif)
El lenguaje de la gráfica de transición quedará expresado por 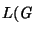 donde
donde
Al calcular la operación ``estrella'', se obtiene
y consecuentemente, el lenguaje reconocido por la gráfica de transición es
Así pues, para una gráfica de transición
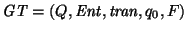 con sólo dos estados q1 y q2. Hagamos
con sólo dos estados q1 y q2. Hagamos
Entonces, de la ec. (4.27) obtenemos:
![$L(\mbox{\it GT\/})=\left[a_{11}^* a_{12} a_{22}^* a_{21}\right]^* a_{11}^*b_1+a_{12} a_{22}^*b_2.$](img1431.gif)
Ejemplo:
Sea
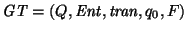 la gráfica de transición vista anteriormente, donde
la gráfica de transición vista anteriormente, donde
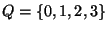 ,
,
 ,
q0=0,
,
q0=0, 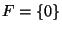 y las transiciones son
y las transiciones son
 .
Al aplicar el algoritmo 4.1 obtenemos la tabla siguiente:
.
Al aplicar el algoritmo 4.1 obtenemos la tabla siguiente:
Por tanto,
y se obtiene el sistema de ecuaciones
Puesto de manera matricial el anterior sistema de ecuaciones queda de la forma![[*]](../images/spanish/icons.gif/foot_motif.gif)
El lenguaje de la gráfica de transición quedará expresado por 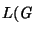 donde
donde
Al calcular la operación ``estrella'', se obtiene
y consecuentemente, el lenguaje reconocido por la gráfica de transición es



Siguiente: Expresiones regulares y sistemas
Un nivel arriba: Expresiones regulares
Anterior: Matrices de expresiones regulares
Guillermo Morales-Luna
2000-06-27
 .
.
 ,
haciendo
,
haciendo
 es equivalente a la gráfica de transición dada
es equivalente a la gráfica de transición dada
 ,
y las partes de Q que son accesibles desde el estado inicial q0 en la gráfica.
Por tanto, podemos calcular al autómata cociente
,
y las partes de Q que son accesibles desde el estado inicial q0 en la gráfica.
Por tanto, podemos calcular al autómata cociente
 de manera similar a como se calcula el autómata equivalente a una gráfica de transición. En la Figura 4.1 presentamos el seudocódigo de este procedimiento.
Si
de manera similar a como se calcula el autómata equivalente a una gráfica de transición. En la Figura 4.1 presentamos el seudocódigo de este procedimiento.
Si
 ,
supongamos que
,
supongamos que
 hacen transitar a
hacen transitar a 
 .
Al aplicar el algoritmo 4.1 obtenemos la tabla siguiente:
.
Al aplicar el algoritmo 4.1 obtenemos la tabla siguiente:
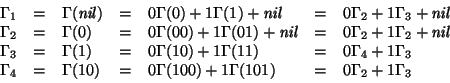
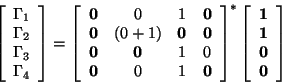
![\begin{displaymath}\left[\begin{array}{c}
\Gamma_1 \\ \Gamma_2 \\ \Gamma_3 \\ \...
...ox{\bf 1} \\ \mbox{\bf0} \\ \mbox{\bf0}
\end{array}\right]
\end{displaymath}](img1435.gif)
![\begin{displaymath}\left[\begin{array}{c}
\Gamma_1 \\ \Gamma_2 \\ \Gamma_3 \\ \...
...ox{\bf 1} \\ \mbox{\bf0} \\ \mbox{\bf0}
\end{array}\right]
\end{displaymath}](img1436.gif)

 .
Al aplicar el algoritmo 4.1 obtenemos la tabla siguiente:
.
Al aplicar el algoritmo 4.1 obtenemos la tabla siguiente:
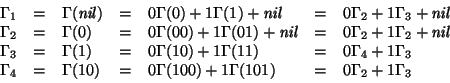
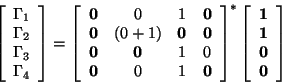
![\begin{displaymath}\left[\begin{array}{c}
\Gamma_1 \\ \Gamma_2 \\ \Gamma_3 \\ \...
...ox{\bf 1} \\ \mbox{\bf0} \\ \mbox{\bf0}
\end{array}\right]
\end{displaymath}](img1435.gif)
![\begin{displaymath}\left[\begin{array}{c}
\Gamma_1 \\ \Gamma_2 \\ \Gamma_3 \\ \...
...ox{\bf 1} \\ \mbox{\bf0} \\ \mbox{\bf0}
\end{array}\right]
\end{displaymath}](img1436.gif)