



Siguiente: Propiedades de lenguajes regulares
Un nivel arriba: Lema de bombeo
Anterior: Ejemplo:
Sea L el lenguaje consistente de las representaciones en binario, sin ceros a la izquierda, de los números primos. L no puede ser regular.
En efecto, supongamos que para todo
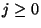
y, por un momento, supongamos que L es regular.
El teorema de Euclides sobre la infinidad de los números primos muestra que en L hay cadenas arbitrariamente largas.
Elijamos n>0 que satisfaga 4.37, y consideremos un primo p>2n, es decir, un primo cuya representación en binario tenga longitud superior a n. Entonces podemos encontrar
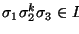 tales que para todo
tales que para todo 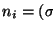 ,
,
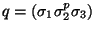 es un número primo.
Sea
es un número primo.
Sea
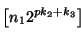 ,
i=1,2,3, el número representado en binario por la partícula
,
i=1,2,3, el número representado en binario por la partícula 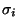 y sea ki la longitud de
y sea ki la longitud de 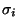 .
Para j=p, el número
.
Para j=p, el número
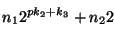 ha de ser primo. Se tiene, al agrupar a la representación en binario de q en un primer bloque a la derecha de k1 bits, p bloques contiguos de k2 bits hacia la izquierda y uno último de k3 bits, que
ha de ser primo. Se tiene, al agrupar a la representación en binario de q en un primer bloque a la derecha de k1 bits, p bloques contiguos de k2 bits hacia la izquierda y uno último de k3 bits, que
Ahora, por el Teorema Pequeño de Fermat,
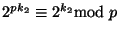 .
Por tanto,
.
Por tanto,
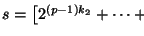 ,
y
,
y
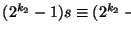 ,
pues
2pk2=2k22(p-1)k2.
Sea
,
pues
2pk2=2k22(p-1)k2.
Sea
![$s=\left[2^{(p-1)k_2}+\cdots+ 2^{k_2} + 1\right]$](img1582.gif) .
Entonces
(2k2- 1)s=2pk2- 1. Por tanto,
.
Entonces
(2k2- 1)s=2pk2- 1. Por tanto,
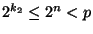 .
Así, módulo p, se tiene las igualdades
.
Así, módulo p, se tiene las igualdades
Por consiguiente p debe dividir a
(2k2- 1) o a (s-1). No puede dividir a
(2k2- 1) pues
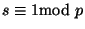 ya que
ya que
 .
Por tanto p debe dividir a s-1. Se sigue que
.
Por tanto p debe dividir a s-1. Se sigue que
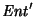 .
Al tomar congruencias módulo p en 4.38 se tiene
.
Al tomar congruencias módulo p en 4.38 se tiene
es decir, el primo q debe ser divisible por el primo p. Esto es una contradicción y por tanto L no puede ser regular.




Siguiente: Propiedades de lenguajes regulares
Un nivel arriba: Lema de bombeo
Anterior: Ejemplo:
Guillermo Morales-Luna
2000-06-27
 .
Por tanto p debe dividir a s-1. Se sigue que
.
Por tanto p debe dividir a s-1. Se sigue que
![\begin{eqnarray*}q &\equiv& \left[n_1 2^{pk_2+k_3} +n_2 2^{k_3}+n_3\right]\mbox{...
...\
&\equiv& p\mbox{\rm mod }p \\
&\equiv& 0\mbox{\rm mod }p
\end{eqnarray*}](img1588.gif)