Tubulating Proper Flexagons

Any tubulating flexagon (that is, one with exposed tubulations, also called an incomplete flexagon) may be made by deleting a given number of sides from a certain complete flexagon of order $N+(F_i-1)$ where $N$ is the order of the tubulating flexagon and $F_i$ is the order of the flex involved in a tubulation. What we want to know now is what effect on the plan this tubulation has. Let us take for an example a complete proper hexaflexagon of order 6 (see figure 8.4a). If we wish to delete a side, say side 5, we fold the two 5's in the plan together. When we do this, we find that the hinge difference across the double leaf is +2 (or $-4$) (See figure 8.4b). Now if we want to delete side 6, fold the 6's together, and the total hinge difference across the triple leaf is $\pm 3$ (see figure 8.4c). If we were to take two hexagonal leaves, each with a hinge difference of +2, (see figure 8.4 d,e), the total hinge difference when the leaves are folded together would be +4 or $-2$. In general, whenever we fold together two leaves with hinge differences respectively of $+a$ and $+b$, the total hinge difference will be $(a+b)$ or $(a+b-G)$. To produce an exposed $n-$flex, we must delete $(n - 1)$ leaves from a complete proper pat, but since each of these leaves has a hinge difference of 1, the total hinge difference across the leaf resulting from the deletions must be $1 \times n$. Therefore, in the plan, an $n-$flex requires a leaf with a hinge difference of $n$.

Example:

Find the plan for the flexagon with the map as shown in figure 8.5a. The method of attack for this problem is to view the tubulating flexagon as a product of the deletion of sides from the flexagon with the map as shown in figure 8.5b. The sign and number sequence for this flexagon will be:

+	+	+	-	-	-	-	-	-	+	+	+	-	-	+
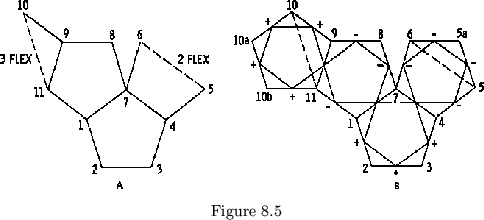
(1)	3	(3)	7	(5a)	5a	(4)	1	(9)	10a	(l0a)	11	(8)	8	(1)
2	(2)	4	(6)	6	(5)	5	(11)	10	(10)	10b	(10b)	9	(7)	2

Now if we delete side $5a$, the hinge difference across the new leaf will be $(-)+(-)$ or $-2$. The process of deleting this side will turn upside down that part of the plan from 5 on:

+	+	+	-	$^-_-$	-	-	+	+	+	+	-	-	+
(1)	3	(3)	7	(5)	5	(11)	10	(10)	10b	(l0b)	9	(7)	(2)
2	(2)	4	(6)	6	(4)	1	(9)	10a	(10a)	11	(8)	8	(1)

The sides $10a$ and $10b$ will be deleted next. The hinge difference across this new leaf will be $(+)+(+)+(+)=$ $\begin{array}[b]{c} + \\ + \\ + \end{array}$ or $\begin{array}[b]{c} - \\ - \\ - \end{array}$, and since there are two deletions in this operation, the part of the plan beyond $11$ will be flipped over and then flipped back:

+	+	+	-	$^-_-$	-	-	+	$^-_-$	-	-	+
(1)	3	(3)	7	(5)	5	(11)	10	(10)	9	(7)	(2)
2	(2)	4	(6)	6	(4)	1	(9)	11	(8)	8	(1)

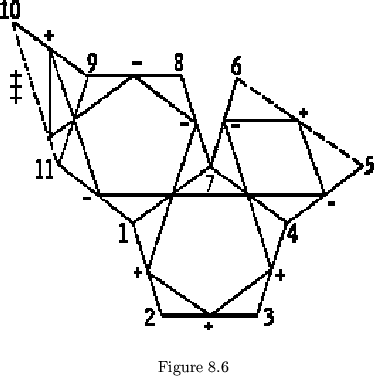
A shortcut that eliminates all of this complex figuring is to draw a polygon system including all tubulations (see figure 8.6). The points in the polygon system which touch tubulations are given values according to the order of the flex the tubulation is, and according to whether the turn is positive or negative. This method produces identical results with the previously mentioned method.