A few things should be noted here about hidden tubulations.
First of all, it is impossible to add another side to a hidden tubulation
of a proper flexagon, for even the ![]() flex leaves more than one leaf in
the left hand pat. This means that if the leaf were slit in order to
open up the new side, one of the original sides would be suppressed and
could not be turned up. Second, as has already been shown, a hidden
tubulation, if flexed through, shortcuts another side, omitting it from
the normal cycle. Many of these tubulations must be forced in order to
shortcut any sides.
flex leaves more than one leaf in
the left hand pat. This means that if the leaf were slit in order to
open up the new side, one of the original sides would be suppressed and
could not be turned up. Second, as has already been shown, a hidden
tubulation, if flexed through, shortcuts another side, omitting it from
the normal cycle. Many of these tubulations must be forced in order to
shortcut any sides.
This is because the sum of the hinge differences about the center does
not equal 360![]() .
However, if we were to make the hinge a number
.
However, if we were to make the hinge a number ![]() hinge,
we would still shortcut one or more sides, depending on the value of
the original tubulation, but we would not have to force this shortcut.
If we are to make an
hinge,
we would still shortcut one or more sides, depending on the value of
the original tubulation, but we would not have to force this shortcut.
If we are to make an ![]() flex into a
flex into a ![]() flex, we must exchange
the two hinges 1 and
flex, we must exchange
the two hinges 1 and ![]() ,
or else we would have two hinges of a kind in the same large pat.
For example, consider a proper complete one cycle pentaflexagon on which we
have reached side 1 after having come from side 5. Instead of 1 flexing
to side 2, we want to
,
or else we would have two hinges of a kind in the same large pat.
For example, consider a proper complete one cycle pentaflexagon on which we
have reached side 1 after having come from side 5. Instead of 1 flexing
to side 2, we want to ![]() flex to side 3. We first must tubulate to side
3 (using a number
flex to side 3. We first must tubulate to side
3 (using a number ![]() hinge), then exchange the hinge between leaves 1
and 2 in the large pat for that between leaves 2 and 3. We can do this by
cutting the two hinges and taping leaves 1 and 2 together with a
hinge), then exchange the hinge between leaves 1
and 2 in the large pat for that between leaves 2 and 3. We can do this by
cutting the two hinges and taping leaves 1 and 2 together with a ![]() hinge
and leaves 2 and 3 with a
hinge
and leaves 2 and 3 with a ![]() hinge. Although the flex we can use to
travel to side 3 is a
hinge. Although the flex we can use to
travel to side 3 is a ![]() flex, the flex leaves two leaves in the left-hand
pat. When rotation is completed this pat will have a hinge in a
flex, the flex leaves two leaves in the left-hand
pat. When rotation is completed this pat will have a hinge in a
![]() position,
because the
position,
because the ![]() flex will have subtracted ``1'' from the hinge values of all
hinges, including the
flex will have subtracted ``1'' from the hinge values of all
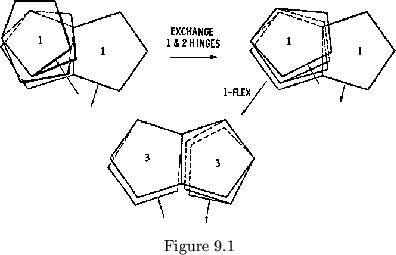
hinges, including the ![]() hinge between leaves 1 and 2. The orientation of
a right pat is opposite that of a left pat, so that the new
hinge between leaves 1 and 2. The orientation of
a right pat is opposite that of a left pat, so that the new ![]() hinge is
to the right of the
hinge is
to the right of the ![]() hinge (see figure 9.1).
hinge (see figure 9.1).
Now, when we ![]() flex again, the flexing operation takes one leaf off
the right hand pat, leaving a single leaf in that pat and exposing
face 2, the face which we originally cut off. After rotation, the hinge
for side 4 is in a number 1 position and the flexagon flexes from the
right pat again, leaving three leaves in that pat. The next flex, which
opens up side 5, is a left-flex, and puts all the leaves except one in the
right pat. The flex after that is also, of necessity, a left flex to side 1,
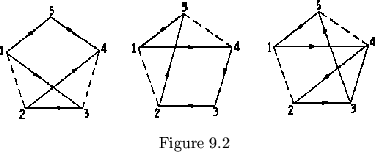
and so starting the cycle over again. The map of this flexagon shown in
figure 9.2a; If the shortcut we wanted
to make had been from 1 to 4, we would
instead exchange the hinges 1 and 3
without altering in any way hinge 2.
The flexagon would then open up to side
4, while leaving three leaves in the
left pat. After rotation, the original
number 2 hinge (attached to side 3), which would have been unchanged by the
exchange of hinges, would be in a 1 position, so the flexing (right) would
open up to side 3. At side 3, the hinge for side 2 will be in the
1 position, there having been 2 flexings since it was in a number 3 position.
After side 2, the hinging was unchanged,
so the next flexes will be 2, 5, 1 and the cycle
will repeat (see figure 9.2b). The thing that is important to notice
is that after an exchange of the two hinges in the proper flexagon, the
succeeding flexes go back to the sides which were originally shortcut,
before proceeding with the rest of the cycle. If, in this last flexagon,
we decide we want to make another shortcut from side 4 to side 2,
omitting side 3 temporarily, we can interchange their respective hinges
(number 1 and number 2), 1 flex to 2, then go back to 3 and from there to
5 to 1 (see figure 9.2c). Thus, we may make any kind of shortcut we
want by simply exchanging two hinges. This interchange of hinges in no
way alters the pat structure of the flexagon-only the hinge sequence.
It should be noticed that there are still hidden tubulations from any
side to all other non-adjacent sides. Those along the outside of the
map polygons are generally indicated with dotted lines, for, as we shall
see, they are quite important.
flex again, the flexing operation takes one leaf off
the right hand pat, leaving a single leaf in that pat and exposing
face 2, the face which we originally cut off. After rotation, the hinge
for side 4 is in a number 1 position and the flexagon flexes from the
right pat again, leaving three leaves in that pat. The next flex, which
opens up side 5, is a left-flex, and puts all the leaves except one in the
right pat. The flex after that is also, of necessity, a left flex to side 1,
and so starting the cycle over again. The map of this flexagon shown in
figure 9.2a; If the shortcut we wanted
to make had been from 1 to 4, we would
instead exchange the hinges 1 and 3
without altering in any way hinge 2.
The flexagon would then open up to side
4, while leaving three leaves in the
left pat. After rotation, the original
number 2 hinge (attached to side 3), which would have been unchanged by the
exchange of hinges, would be in a 1 position, so the flexing (right) would
open up to side 3. At side 3, the hinge for side 2 will be in the
1 position, there having been 2 flexings since it was in a number 3 position.
After side 2, the hinging was unchanged,
so the next flexes will be 2, 5, 1 and the cycle
will repeat (see figure 9.2b). The thing that is important to notice
is that after an exchange of the two hinges in the proper flexagon, the
succeeding flexes go back to the sides which were originally shortcut,
before proceeding with the rest of the cycle. If, in this last flexagon,
we decide we want to make another shortcut from side 4 to side 2,
omitting side 3 temporarily, we can interchange their respective hinges
(number 1 and number 2), 1 flex to 2, then go back to 3 and from there to
5 to 1 (see figure 9.2c). Thus, we may make any kind of shortcut we
want by simply exchanging two hinges. This interchange of hinges in no
way alters the pat structure of the flexagon-only the hinge sequence.
It should be noticed that there are still hidden tubulations from any
side to all other non-adjacent sides. Those along the outside of the
map polygons are generally indicated with dotted lines, for, as we shall
see, they are quite important.
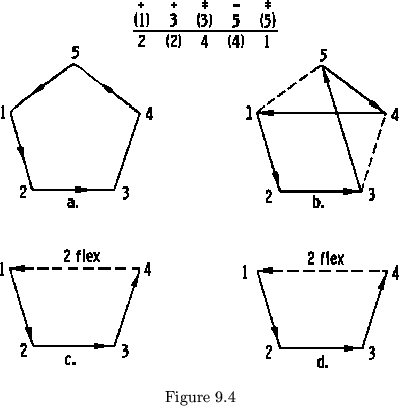
Given the hinge sequence and the pat structure, it is possible to find the plan. Let us examine the plan of a proper flexagon whose hinges have been interchanged. Take as an example the flexagon in figure 9.2a. The proper flexagon from which this one was made had this constant order and hinge sequence:
| 0 1 2 3 4 0 | Hinge sequence |
| 5-1 2 3 4; 5-1 | Pat structure |
The sides of that flexagon were associated with the leaves of the pat in this manner:
| 5-1 2 3 4; 5-1 | Pat structure |
| 1 2 3 4 5 1 | Basic number sequence |
The hinges of sides 2 and 3 were then exchanged. This means that we can find the new hinge sequence by exchanging the numbers in the hinge sequence corresponding to these sides:
| Exchanged hinges | |
| 0 2 1 3 4 0 | Hinge sequence |
| 5-1 2 3 4; 5-1 | Pat structure |
| 1 2 3 4 5 1 | Basic number sequence |
or, since the hinge between leaf 1 and 2 is identified with leaf 1, by convention, and since leaf 1 is also identified with the first number of the basic number sequence, we may write this:
| 0 2 1 3 4 0 | Hinge sequence |
| 5 1 2 3 4; 5 | Pat structure |
| 5 1 2 3 4 5 | Basic number sequence |
We may now obtain the hinge difference and then the sign sequence from this:
| 0 | 2 | 1 | 3 | 4 | 0 | Hinge sequence |
| 2 | 4 | 2 | 1 | 1 | Hinge difference | |
| 5 | 1 | 2 | 3 | 4 | 5 | Basic number sequence |
which gives:
| - | + | + | |||
| (1) | 3 | (3) | 5 | (5) | 2 |
| 2 | (2) | 4 | (4) | 1 | (1) |
from which we get the plan.
This flexagon differs from the proper flexagon in that the hinge
sequence is not consecutive for one cycle. Any flexagon which is not
basically consecutive in some part of its hinge structure and is not a
product of deleting sides from such a flexagon is an
improper flexagon. It
is quite possible for an improper flexagon to have a pat structure
identical with either proper complete or proper incomplete (tubulating)
flexagons. There are no improper triflexagons, and just one improper
tetraflexagon of one cycle, but there are three improper pentaflexagons
of one cycle, eleven improper hexa-flexagons of one cycle and forty-two
improper heptaflexagons of one cycle (see figure 9.3).
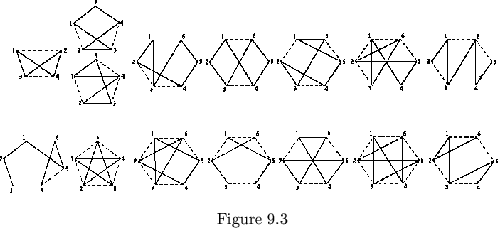
We have been able to make proper flexagons with any desired map by simply
slitting single leaves of a flexagon of lower order.
How can this be done with improper flexagons? Let us take two pentaflexagons
one proper and one improper (see figure 9.4 a & b) and delete sides 5 and
4 respectively by paper clipping the leaves together. The maps of these two
deleted flexagons will be identical except for a minor difference in
numbering (sec figure 9.4 c & d). Now, if we wish
to reopen the missing side we have a number
of choices (four to be exact), as we saw in
Chapter VI. We will consider two of them,
one being slitting the left most leaf, and
the other slitting the right most leaf. If
the left hand leaf is slit, the flexing
operation can remove all but one of the
leaves from the left pat and deposit them
uninverted on the inverted right pat. In the next flex,
the thumbhole associated with side 1 will open up, taking all the leaves off
the left pat, since it is the uppermost thumbhole. If the right leaf were
slit, the following flex would take the bottom leaf off the right pat and
place it on the inverted left pat. The rotation will
necessitate a right flex, involving the hinge which was originally in a
![]() position, i.e. the hinge associated with side 1.
However, the order of the thumbholes has been reversed by the pat inversion
of previous right flex, so instead of being the top thumbhole, the side 1
thumbhole is going to be on the bottom, and the next right-flex is only
going to add one leaf to the left pat, and will invert the remainder of the
right pat. The thumbhole adjacent to the one associated with side 1 is
associated with side 2 and also was originally hinged in a 3-position.
After two flexes it will be hinged with a
position, i.e. the hinge associated with side 1.
However, the order of the thumbholes has been reversed by the pat inversion
of previous right flex, so instead of being the top thumbhole, the side 1
thumbhole is going to be on the bottom, and the next right-flex is only
going to add one leaf to the left pat, and will invert the remainder of the
right pat. The thumbhole adjacent to the one associated with side 1 is
associated with side 2 and also was originally hinged in a 3-position.
After two flexes it will be hinged with a ![]() hinge, and having
been inverted twice, it will be the top thumbhole.
The flexing operation exposing side 2 will remove the
remainder of the leaves from the left pat and place them on the right pat,
preparing for another left flex. Thus, in constructing a flexagon,
whenever we have two choices in slitting to get a new side, slitting
the single left leaf exposed by the tubulation will produce a proper
portion of a cycle, while slitting a single leaf in the other pat will
give an improper portion of a cycle.
hinge, and having
been inverted twice, it will be the top thumbhole.
The flexing operation exposing side 2 will remove the
remainder of the leaves from the left pat and place them on the right pat,
preparing for another left flex. Thus, in constructing a flexagon,
whenever we have two choices in slitting to get a new side, slitting
the single left leaf exposed by the tubulation will produce a proper
portion of a cycle, while slitting a single leaf in the other pat will
give an improper portion of a cycle.
There are certain basic characteristics of the improper flexagon.
It has the same pat structure, the same map (except for order of flexes),
and hence the same number sequence as the corresponding proper flexagon.
It will be found, of course, that the proper flexagon with the same
pat structure as an improper flexagon has an identical polygon system.
Since an improper flexagon is not constantly a left or right flexing
flexagon, the thumbholes do not necessarily have to be in one pat. The
number of thumbholes in a folded unit, however, is always equal to ![]() .
.