Detecting transitive behavior in
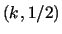 reversible one dimensional cellular automata
reversible one dimensional cellular automata
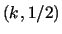 reversible one dimensional cellular automata
reversible one dimensional cellular automata
Using the process presented in section 5.4, we can define a transition relation among sequences ![]() in the set
in the set ![]() . In this way, we have a surjective mapping from the set
. In this way, we have a surjective mapping from the set ![]() to itself, since every sequence has at least one ancestor. In this transition relation, the indices are sequences
to itself, since every sequence has at least one ancestor. In this transition relation, the indices are sequences ![]() of
of ![]() cells and the elements show the mapping from one sequence
cells and the elements show the mapping from one sequence ![]() to a set of sequences
to a set of sequences ![]() as is presented in Table 2.
as is presented in Table 2.
|
As in the connectivity relation defined in Table 1, we can do the transitive closure of the transition relation. Depending of the number of classes that we get with this process, we will detect different kinds of transitive behavior among centered cylinder sets defined by sequences in the set ![]() .
.
In the configuration space
![]() , if a
, if a
![]() reversible one dimensional cellular automaton defines a topologically ergodic dynamical system then for every
reversible one dimensional cellular automaton defines a topologically ergodic dynamical system then for every
![]() , there exists a configuration
, there exists a configuration ![]() which belongs to the centered cylinder set
which belongs to the centered cylinder set
![]() and it has an orbit through all the other centered cylinder sets defined by the sequences in the set
and it has an orbit through all the other centered cylinder sets defined by the sequences in the set ![]() . Thus, a consequence of Lemma 1 is the following:
. Thus, a consequence of Lemma 1 is the following:
Finally, the transition relation and its transitive closure give us important information about the mixing behavior of
![]() reversible one dimensional cellular automata. In the transition relation, the
reversible one dimensional cellular automata. In the transition relation, the ![]() in the principal diagonal indicate centered cylinder sets which can return to the same centered cylinder set in one step. In other words, the principal diagonal shows centered cylinder sets that can be fixed.
in the principal diagonal indicate centered cylinder sets which can return to the same centered cylinder set in one step. In other words, the principal diagonal shows centered cylinder sets that can be fixed.
Using the principal diagonal and the transitive closure of the transition relation, we have the following result:
In this way, we have defined simple matrix methods that using the properties of block permutations and transitive closures detect periodical and transitive behavior. Of course, a big problem is that these methods only detect the existence of these orbits but they doesn't give an explicit example of them.