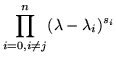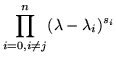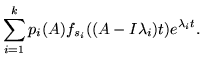Next: Leonard, Maki, and three
Up: A chain of references
Previous: Moler and van Loan
Shortly after Putzer's article appeared, and in direct reference to it, R. B. Kirchner's article [20] ``An explicit formula for eAt,'' defined some interpolation polynomials and showed that they could be used to get Putzer's result, all the while satisfying the differential equation for an exponential. He defined interpolation polynomials
 |
= |
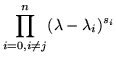 |
(27) |
together with their sum,
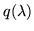 |
= |
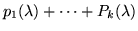 |
(28) |
and claimed that since
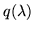 has no roots in common with the characteristic polynomial, then by using the the Euclidean algorithm on the combination of q and characteristic polynomial, the matrix q(A) is invertible. In other words, q is not necessarily a resolution of the identity, but it is the next best thing and can be used to derive an analogue of Sylvester's formula,
has no roots in common with the characteristic polynomial, then by using the the Euclidean algorithm on the combination of q and characteristic polynomial, the matrix q(A) is invertible. In other words, q is not necessarily a resolution of the identity, but it is the next best thing and can be used to derive an analogue of Sylvester's formula,
| q(A)eAT |
= |
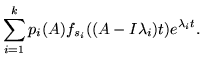 |
(29) |
The functions fsi are just the leading terms in the power series expansion for eX and contribute the derivatives already seen in Sylvester's formula. In fact, the main difference between Kirchner's presentation and the one given in our own report lies in his use of powers to define the interpolation polynomials whilst our definition derived from a partial fraction decomposition and avoided the intervention of q(A) in the formula.
This difference in approach is akin to the fololowing choice. Suppose that a confluent form of Lagrange interpolation is to be used at two points. The basis ploynomials at either point can consist of powere, or something else. Likewise the dual basis at the two points consist of derivatives or something else. Depending on the preference for derivatives or for powers at each point, four different interpolation formulas can result.




Next: Leonard, Maki, and three
Up: A chain of references
Previous: Moler and van Loan
root
2000-03-17