Glider collisions

**Figure:** B collisions always promote E_n to E_n+1, but there are some A collisions which will restore the count, reducing E_n to E_n-1 or at the bottom of the chain, E to C.
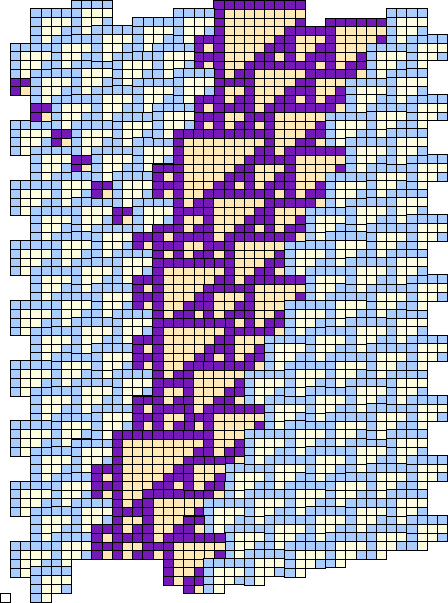
$\begin{figure} \centering \begin{picture} (300,400) \put(0,0){\epsfxsize=300pt \epsffile{edecr.eps}} \end{picture} \end{figure}$

Cook recognizes at least seven types of gliders, some of which have multiple variants, and all of which can be packed in various combinations. Glider technology consists in exploiting collisions. It is readily seen that there are fifty or more, actually in the hundreds or thousands, of binary collisions. From there on the numbers are much larger. Although that forebodes a mass of data, there is an element of hope.

**Figure:** Some of the glider collisions involving the three different embedments of the C glider in the ether on the one hand, and members of the family E, EBar, and F in each of their two alignments relative to the C's. The labels are Cook's.
$\begin{figure} \centering \begin{picture} (300,225) \put(0,0){\epsfxsize=300pt \epsffile{clls.eps}} \end{picture} \end{figure}$

Even though a dozen or two of gliders seems like a large number, that is far fewer than the number of possible collisions. Either collisions will produce multiple reaction products, or many collisions will end up producing identical results. Both alternatives coexist, but one of the fortunate combinations leaves the reactants unchanged, just that they chang places. That is a soliton reaction, useful for moving information from one place to another across intervening barriers.

Actually we didn't discover this for ourselves, but only as a result of a hint from Cook. That, and the general knowledge that it would eventually be necessary to examine the collisions in one way or another.

**Figure:** Left: In the collision of an F glider with the stationary C1, the glider sails on past. Right: Two C2's decrement an E_n to ,E_n-1.
$\begin{figure} \centering \begin{picture} (430,520) \put(0,0){\epsfxsize=210pt \... ...}} \put(220,0){\epsfxsize=210pt \epsffile{edown.eps}} \end{picture} \end{figure}$

**Figure:** Left: C2E_nHi collisions result in n B gliders which can interact with new C's to recreate E_n-1 gliders. Right: C3E_nHi collisions release n+1 gliders which can be used to restore the E_n.
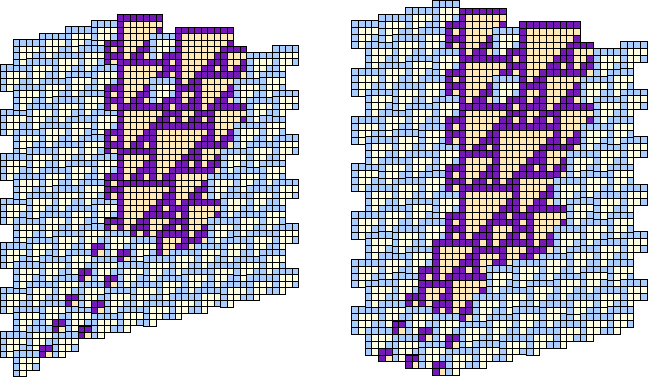
$\begin{figure} \centering \begin{picture} (430,250) \put(0,0){\epsfxsize=210pt \... ...} \put(220,0){\epsfxsize=210pt \epsffile{c3e2hi.eps}} \end{picture} \end{figure}$

**Figure:** A partial listing of the products of C and E collisions. All the C2 and C3 collisions in the high position are clean, releasing nothing more than a flotilla of B gliders.
$\begin{figure} \centering \begin{picture} (210,230) \put(0,0){\epsfxsize=210pt \epsffile{CEN.eps}} \end{picture} \end{figure}$

Part of the understanding of E and G collisions is that the leading triangles are escorting $\alpha$ gliders in one constellation or another; when the escort is damaged by a collision, the result is a typical putrefaction of an $\alpha$ lattice, for which the rules of engagement can be worked out.