Speed limits

Gliders in automata cannot have superluminal velocities because their configurations are determined by a function, and therefore deterministic once an initial neighborhood has been specified. This prohibition is inoperative at light velocity or less, but there may be other considerations limiting velocities. For example, in Life there are infinite patterns moving at light velocity, any of the ripples derived from the one-dimensional Rule 22. But restricting the extent of the live part of the configuration reduces the velocity, which was one of the first charasteristics mentioned when Life was first publicized.

Gliders relative to the ether seem to obey similar restrictions, evidences of which can be seen by examining Cook's list of known gliders. A's and B's are the fastest; A's and D's are the only ones with positive velocities. There are gliders which he called BBar, which have the same velocity as the B gliders, but which take a multiple of the B period to complete their own period. But there are no ABars, and no BDoubleBars.

His glider list, which others claim to have verified by their own search programs, is an empirical result. There are different kinds of search programs; one which we used to list cycles in Rule 22 up to length 34 should be able to detect Cook's gliders, but we have not tried to revive the older computers on which it was run.

Another approach is to filter the shift-periodic de Bruijn diagrams down to their ergodic nuclei, to see which combinations could be gliders. This approach is quite reliable, but the size of the diagrams to which it is to be applied are enormous; about ten generations is the limit for present computer speed and memory, although it could be stretched somewhat given sufficient incentive. But that region only contains A, B, C, and D gliders; BBar, E, F, and G lie on beyond, some of them quite a bit.

**Figure:** A possible speed limit. There is a transition region between a glider and the ambient lattice. If a glider is to move faster than an A glider, there will be an ether margin with a little hook in it, whose filling could have restrictive repercussions.
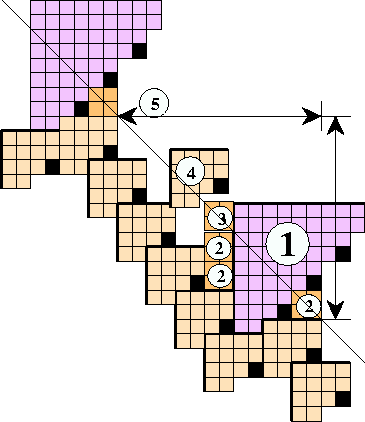
$\begin{figure} \centering \begin{picture} (250,300) \put(0,0){\epsfxsize=250pt \epsffile{14in14.eps}} \end{picture} \end{figure}$

To describe a velocity as a class, including all te possible multiples of the basic period and the deviations which only return to the original form after many intervals, another approach is needed. One idea is shown in Figure 15, to take advantage of the little hook sitting on the margin of a strip containing a faster glider than the A. The consequences of filling the niche with tiles of different sizes can be followed down in one of those search trees which is so characteristic of applied Artificial Intelligence.

Two T0's would violate the prohibition against extending top margins, so the smallest viable candidate would be a T1 and if that ran back along the margin, the result would simply be an A glider. If something faster is required, that chain simply creates a new hook, so it is time to move on to the next possibility.

Figure 15 shows the initial consequences of starting with a T8 (1). That immediately forces three T1's (2), following which a fourth T1 can not be stacked alongside the T* (3). Backtracking, it is seen that a T3 could be inserted, based in the next column to the left (4). A new hook is created so it is time to begin again. Eventually the consequences of the original choice must be faced (5) in the form of a wall of some nature. If it is compatible with the procedure to date, the filling of the area above the lower margin of the glider strip is continued until the top margin is encountered.

Hopefully a decision will have been reached before the top margin is required, because there is really no way of knowing how wide a glider strip could be. For evidence, consider the infinitude of A polymers which is possible.

**Figure:** Taking advantage of the kink in the ether margin, and looking at it from the right angle, it becomes plausible that there are no right runners faster than A's nor leftrunners faster than B's.
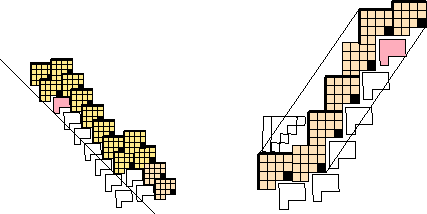$\begin{figure} \centering \begin{picture} (280,150) \put(0,0){\epsfxsize=120pt \... ...}} \put(160,0){\epsfxsize=120pt \epsffile{fleft.eps}} \end{picture} \end{figure}$

The search scheme depicted in Figure 15 may or may not succeed, but there is no denying that it is cumbersome. Figure 16 shows the ether margin from another perspective, which strongly invites the conclusion that nothing can be fitted into the nooks and crannies, rendering any search for faster gliders futile.