| M | = | 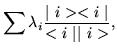 |
(3) |
Using the Dirac bra and ket notation for row and column vectors, the spectral theorem for matrices says that
It is a short step from the spectral theorem to Sylvester's formula,
When a matrix is not normal, it can often be approximated by a parameterized normal matrix whose limit provides a formula involving derivatives of the function as well:
The formula can be established algebraically without taking limits and derivatives, although some preparation is required. Using limits illuminates the origin of the idempotent Ni(0) and nilpotent
![]() 's, but does not give the preferred derivation because of the wide variety of limits which can result. At the level of the spectral theorem the additional structure in the formula it is equivalent to recognizing the Jordan canonical form, and at the level of Sylvester's formula, treats matrix functions with full generality.
's, but does not give the preferred derivation because of the wide variety of limits which can result. At the level of the spectral theorem the additional structure in the formula it is equivalent to recognizing the Jordan canonical form, and at the level of Sylvester's formula, treats matrix functions with full generality.
The full development of the Jordan form is considered to be an advanced topic which is avoided in contexts where it is not necessary (quantum mechanics, which thrives on Hermitean matrices, or introductory books on linear algebra), and often surrounded by much datail when it is actually needed. One of the best of these detailed treatments is Gantmacher's two volume presentation of matrix theory [31]. Although the Jordan form is developed very carefully, Sylvester's formula is left at the level of ``Sylvester-Lagrange interpolation'' and ``elementary divisors;'' but what is needed is a more explicit representation of the Ni(k)'s and their multiplication table.