 |
The difference between a computer and a calculator is that the latter follows a determined sequence of instructions, even if it is the operator who decides the sequence. A computer is capable of taking decisions, often as not based on the sign of a result, as to which of two alternative courses of action to follow. Nearly always, one of the alternatives will be to go back and repeat a previous sequence, a retrograde step in an otherwise forwardleading sequence.
Going back, in a glider based environment such as Rule 110, would imply countermovement in addition to whatever process was bringing instructions and data together. Skipping backwards is equivalent to skipping forward if the instruction stream is repeated periodically and unwanted instructions can be erased, or ignored, or whatever.
That is the reason that discovery of the (A trimer, EBar, D1) leapfrog has such importance for setting up a computer based on Rule 110. Dilligent search had revealed some simple solitons, built up out of combinations of C, EBar and F gliders. Using both EBar's and F's is unwieldy because of their differing velocities, whereas the C's are stable and could reasonably be taken as program elements.
The other glider could represent data and be passed through the instructions, then stopped at their far end and turned into a new program element through glider collisions. Several candididates had been discovered and cataloged. Stoppage implies a flow of gliders from the left which had to be independent of the data which it had to stop, implying further structure to any prospective computing environment.
Thus the importance of either selectively eliminating gliders arriving from the right, or the rightmost static gliders which they were going to meet. That the (A trimer, D1, EBar) combination was overlooked provides an object lesson in dilligence and careful observation. Consulting the catalog of collisions [8] the paragraph dedicated to (D, EBar) collisions is empty, due to its falling at the end of the alphabet and laziness. A more carefully done Atlas [10] contains the collisions, but by then checking collision sequences wasn't being followed out to the necessary conclusion.
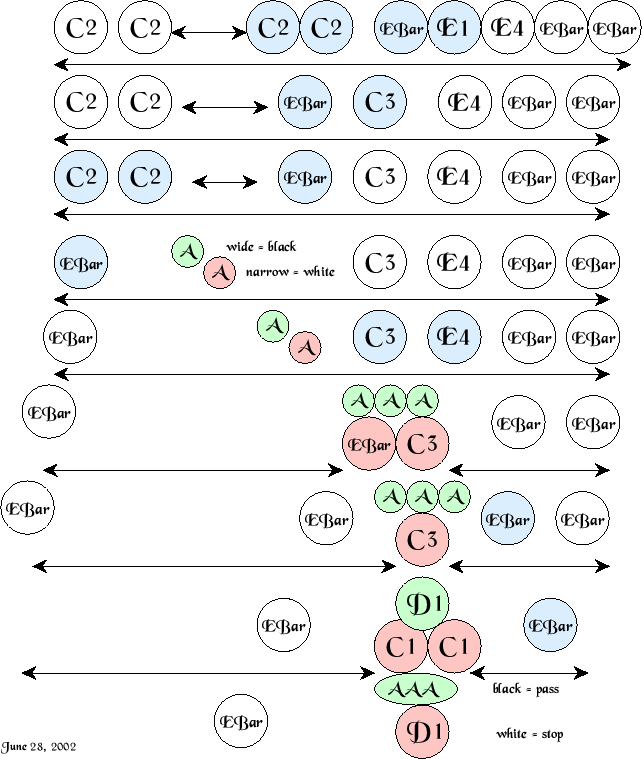
Viewing the drawings in [19] revealed one solution to the problem, from which a consultation of the table of (C, E) collisions (as in Table 2) singles out C2 gliders as the stationary elements. Fortunately, EBar's turn into C2's under many A collisions (see Table 1) which could inhabit the western badlands - the remote left environment.
But now, given that only one kind of glider could be static, and one other kind mobile, the predicate necessary to switch the flow of computation cannot reside in the selection of glider. The spacing between C2's must conform to the phase of the EBar gliders with which they will interact, but variation in terms of the EBar unit cell is still available. So, the spacing between gliders is the next detail that ought to be examined.
The combination finally used by the Cyclic Tag System is intricate indeed, drawing in some ancillary E gliders to absorb stray sparks or provide some of their own. Some nine stages are involved, shown in greater detail on the following pages, beginning with a map of the first few.
 |
 |
 |
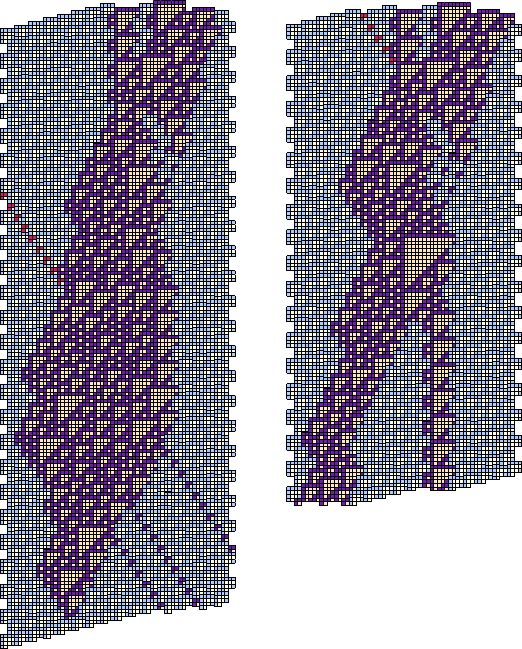 |
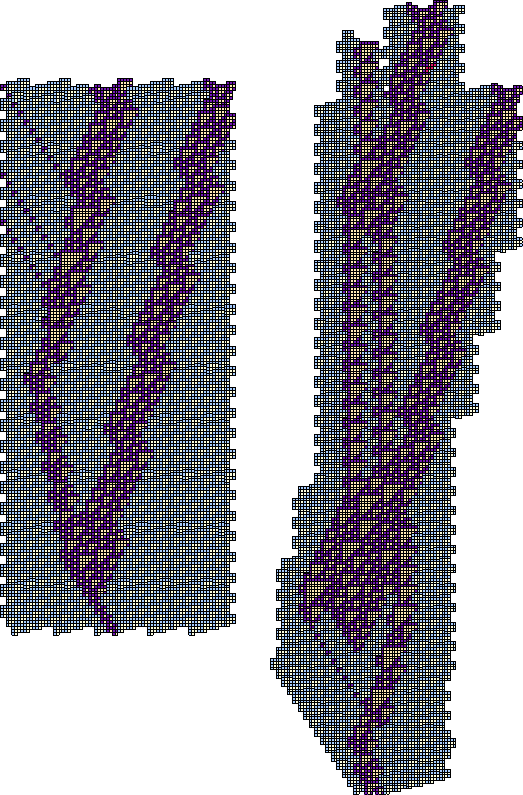 |
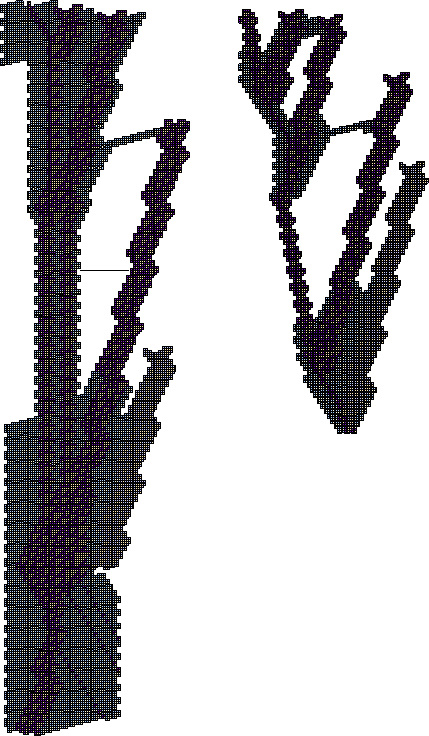 |