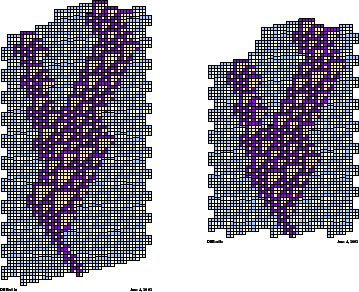A Starting Point: Erasing Unwanted Gliders

Parity makes it difficult to selectively remove structures because almost all gliders are odd and will either pass by another odd object in soliton fashion, leave another pair of gliders, or fizzle out in A's and B's. Removing some without a trace while passing others unimpeded is hard or impossible to arrange; an interesting one has an A trimer colliding with an EBar to produce a D, which collides with another EBar to restore the original A trimer.

Figure 10: The two (D1, EBar) collisions which might participate in the leapfrog.

Figure 11: The three (A trimer, EBar) collision candidates for the leapfrog.

Of the eight (D1, EBar) collisions, two lead to A trimers; both arrive at the same position on the EBar (Fig. 10). Of six collisions with the A trimer, three result in D1's (Fig. 11).

Figure 12 shows one leapfrog erasing three successive EBar's.

Figure 12: One of the requirements of a tag system is the ability to erase structures, be they oncoming EBar packets, or static C groupings. The (A trimer, D) leapfrog will erase all incoming EBars, so long as they are synchronized with the A-D erasure stream.

Eventually, of course, the leapfrog chain has to be terminated. Since the termination has to stop the other leapfrog, which is the sieve which allows some EBar's to pass, it is better to defer its presentation until the controlling predicate has been analyzed; see Figure 21.