![]()
El desarrollo de los Autómatas Celulares (AC), ha tenido tres etapas importantes; la
etapa de John von Neumann a principios de los 50's, von Neumann buscaba la
auto-reproducción de las máquinas, recuérdese que era la época de la postguerra; como
von Neumann carecía de los materiales suficientes siguió la sugerencia de su amigo
Stanislaw Ulam para desarrollar un modelo matemático con el cual pudiera demostrar su
teoría, con ello se sentaron las bases del estudio de los AC.
La segunda etapa importante vino en los 70's con el desarrollo del juego de Life,
por parte de John Conway, el cual podía simular evoluciones interesantes de
"seres" a través de un tiempo dado en un espacio bidimensional utilizando
conceptos de los AC.
La tercera etapa importante vino a mediados de los 80's con las investigaciones
realizadas por Stephen Wolfram [1] sobre los
Autómatas Celulares Lineales (ACL), donde plantea una clasificación en cuatro clases
dependiendiendo del comportamiento que muestran:
Clase I. AC que evolucionan en un estado uniforme.
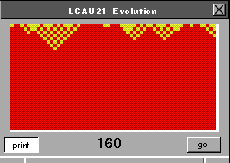
Clase II. AC que evolucionan en estados cíclicos aislados.
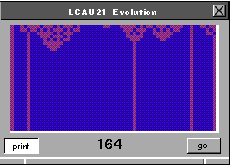
Clase III. AC que evolucionan en comportamientos caóticos.
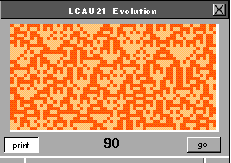
Clase IV. AC que evolucionan en estados complejos aislados.
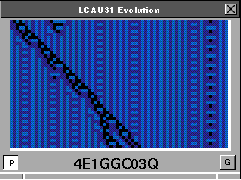
El ACL consiste en un conjunto de células conectadas linealmente, cada célula puede
tener el valor de un número finito de estados y una función de transición (regla de
evolución), la cual hace mapeos locales entre estos estados en unidades de tiempo
discreto.
Un ACL denota su número de estados por k y el radio de la vecindad por r.
La evolución del ACL depende de la función de transición y de la configuración inicial
(primer arreglo de células). Para ejemplificar los conceptos dados anteriormente se
tomará un autómata (2,1), k=2 estados, r=1 vecino de cada lado.
Las diferentes vecindades que existen para este autómata están dadas por:
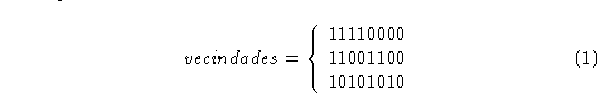
La regla de evolución especifica en que estado evoluciona cada vecindad, para este autómata la regla se denomina en valores binarios que van del 0 al 255 (en decimal, ya que hay 256 combinaciones diferentes), números de Wolfram [1], tomemos la regla 15.
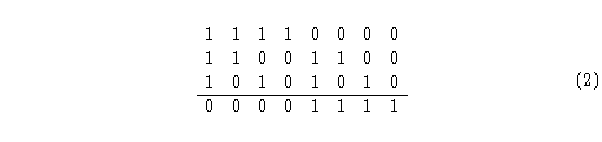
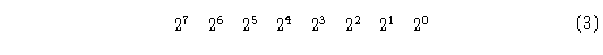
![]()
Tomando una configuración inicial aleatoria, se observará como evoluciona a través
del tiempo con esta regla.
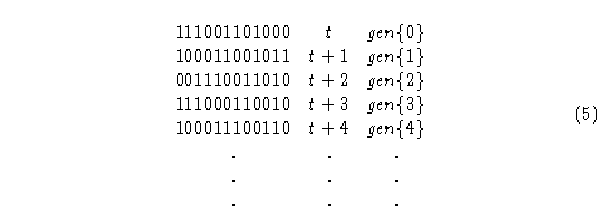
Las configuraciones que puede tener un autómata pueden ser de 3 tipos:
i) Configuraciones que no pueden ser generadas por su regla de evolución y que sólo
pueden aparecer en su configuración inicial. A estas configuraciones sin pasado se les
denomina pertenecientes al Jardín del Edén.
ii) Configuraciones en el tiempo t que pueden ser generadas por diferentes
configuraciones en el tiempo t-1, es decir, tienen múltiples ancestros. Ancestro
es una configuración en el tiempo t-1 que genera la nueva configuración en el
tiempo t.
iii) Configuraciones que son generadas por un ancestro único.
En particular un autómata que genera configuraciones del tipo iii), se les denomina
Autómata Celular Lineal Reversible (ACLR), ya que al tener cada configuración un
ancestro único, éste puede obtenerse mediante una regla inversa de evolución que
revierte el proceso.
![]()
Seck Tuoh Mora Juan Carlos
E-mail:seck@delta.cs.cinvestav.mx