![]()
La aplicación de Teoría de Gráficas juegan un papel importante en el estudio de los
AC, existen tres gráficas que son fundamentales, estas son el diagrama de de Bruijn,
el diagrama de Subconjuntos y el diagrama de Parejas. Una revisión
detallada de muchas de las posibles aplicaciones de éstas en el estudio de AC ha sido
publicada por McIntosh [2].
El diagrama de de Bruijn es una gráfica cuyos nodos son secuencias de símbolos
de algún alfabeto, en este caso el conjunto de estados del autómata. Todas estas
secuencias tienen la misma longitud, para un autómata éstas serían vecindades
parciales, en una dimensión, el estado de una célula liga de un extremo a otro un
vecindario dado.
En principio tal diagrama podría ser extendido a autómatas de mayores dimensiones,
pero un problema surge con la selección de los vecindarios parciales para los nodos del
diagrama, para los cuales su unión formará los vecindarios completos en todas
direcciones; pero al menos en una dimensión no hay ninguna dificultad en crear el
diagrama de de Bruijn.
El número de nodos del diagrama de de Bruijn está dado por k^(2r) y el
número de ligas por k^(2r+1). Ya que los nodos representan fracciones de las
vecindades que tenga el autómata, habrá una liga del nodo i al nodo j, si
y sólo si, la salida del nodo i coincida con la entrada del nodo j (como
fichas de dominó), de esta forma, las características de la evolución pueden ser usadas
para seleccionar subgráficas del diagrama de de Bruijn, por ejemplo; aquella
subgráfica compuesta de las vecindades, cuya célula central nunca cambia si tales
vecindades existen.
El diagrama de de Bruijn transforma el problema del autómata en un problema de
trazo de rutas, por ejemplo; ningún loop puede ser más largo que el número total de
nodos en la gráfica sin repetir algún segmento. Ya que los símbolos son enteros
consecutivos pueden ser tratados como elementos de un anillo o quizás de un campo finito.
La discusión de sus propiedades aritméticas o algebraicas es muy valiosa, por ejemplo;
la matriz de conectividad de diagrama se convierte simplemente en,
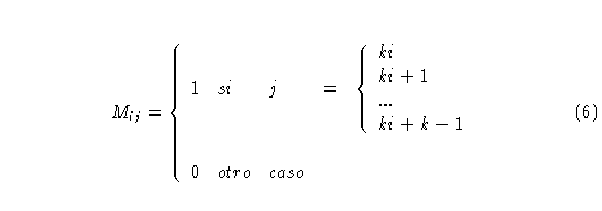
![]()
Seck Tuoh Mora Juan Carlos
E-mail:seck@delta.cs.cinvestav.mx