![]()
En 1991, David Hillman [9] propone un algoritmo
para encontrar ACLR con k estados y un radio de vecindad r.
Hillman hace notar que la reversibilidad no sólo depende de la regla de evolución,
sino también del ancho del anillo del autómata, es decir, el número de células en cada
configuración; así, un autómata puede ser reversible si su ancho es par o non o
múltiplo de algún número.
Algoritmo de Hillman
Sea C una cadena de x células en el tiempo t, de este modo, C
está completamente determinado por la cadena de células P de longitud x+d-1,
en el tiempo t-1, donde d es el tamaño de la vecindad del autómata.
a) Si
![]()
es la configuración en C , sea
![]()
el conjunto de configuraciones las cuales de acuerdo a la regla de evolución, generan
![]()
b) Sea
![]()
la j -ésima configuración presente en
![]()
tomando ésto, formar una tabla
![]()
la cual, su j -ésimo elemento será igual a
![]()
donde
![]()
es el conjunto de las primeras d-1 células en
![]()
es el conjunto de las últimas d-1 células en
![]()
c)Por último, formar
![]()
como el conjunto de todas las tablas
![]()
posibles dado un ancho w. Si w es mayor que 1 ,
![]()
se obtiene de la concatenación de
![]()
para cada elemento
![]()
uno obtiene un elemento
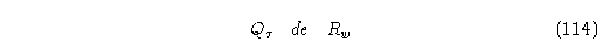
después de comparar cada entrada
![]()
![]()
anadir a
![]()
una entrada m tal que
![]()
El proceso recursivo empieza calculando
![]()
directamente de la regla de evolución.
d) Los elementos

con las listas de las primeras y las últimas d-1 células de cada ancestro de una cadena de longitud w dada. Las primeras d-1 células deben ser iguales a las últimas d-1 células si existe un ancestro, ya que su ancho será de w+d-1 . Así, el j -ésimo ancestro existirá si y solo si
![]()
por lo tanto, si el autómata es reversible, cada tabla
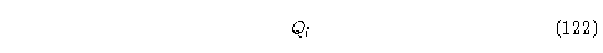
debe tener una y solo una entrada
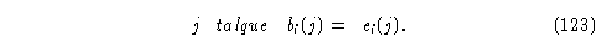
e) El algoritmo para hasta un ancho w especificado.
Como w puede llegar a ser muy grande, el cómputo de
![]()
puede no ser práctico, sin embargo, existen dos propiedades importantes que agilizan
grandemente el cálculo.
1.- Si las tablas en
![]()
no tienen todas el mismo número de elementos, el autómata no es reversible si su ancho es mayor o igual que i+d-1.
2.- Un elemento
![]()
con x menor que z; por lo que el cálculo de las
![]()
se minimiza.
![]()
Seck Tuoh Mora Juan Carlos
E-mail:seck@delta.cs.cinvestav.mx