![]()
Estudiemos ahora un ACL(4,h), con una regla de evolución 05AF05EB.
Regla de evolución.
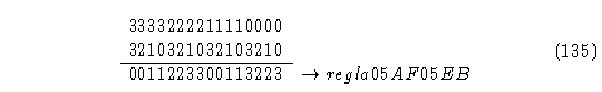
Construyendo las tablas.
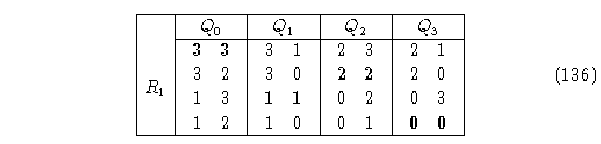
Concatenando R_(1) con R_(1) tenemos:
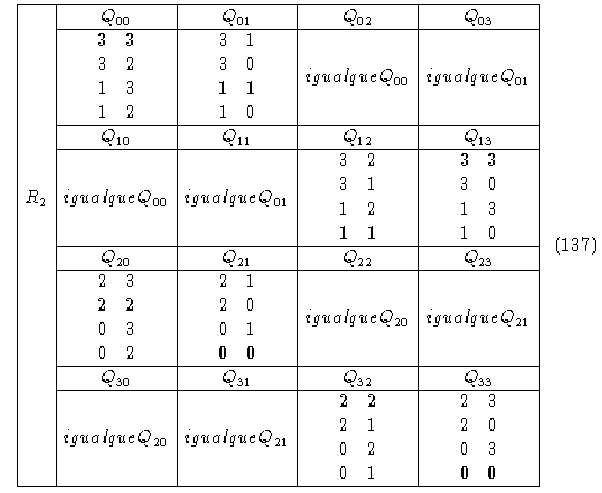
R_(3) se construye de manera análoga.
Según el algoritmo, el ACL parece ser reversible, sin embargo, tomemos las siguientes vecindades y sus evoluciones.
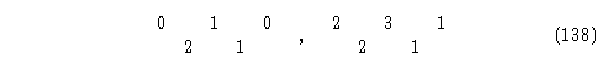
Se observa que la vecindad 21 evoluciona en el pasado con 1 y con 3, lo que es
imposible si el autómata es reversible. Lo que sucede aquí no es que el algoritmo esté
equivocado, sino que es algo muy sutil, el autómata si es reversible, pero la regla de
evolución inversa no tiene un radio de vecindad h, más bien maneja un radio de
vecindad 1, es decir, 1 vecino a cada lado.
Por consiguiente, el tamaño de vecindad de la regla inversa es 3; tomemos las matrices de conectividad del autómata (4,h) con la regla 05AF05EB.
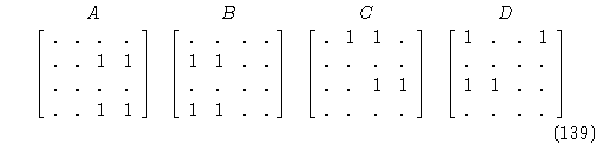
Con ellas encontraremos la evolución hacia atrás para cada una de las posibles
vecindades de tamaño 3 de la regla inversa, utilizando una extensión del algoritmo de
matrices de conectividad.
a) Se toma la vecindad 221.
b) Matriz del elemento 2.
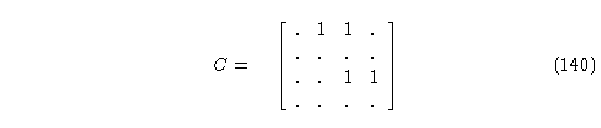
Columnas con suma de elementos diferentes de cero: 1, 2 y 3.
c) Matriz del elemento 2.
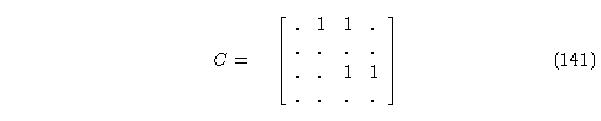
Renglones con suma de elementos diferentes de cero: 0 y 2.
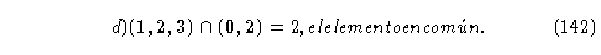
e) Matriz del elemento 2.
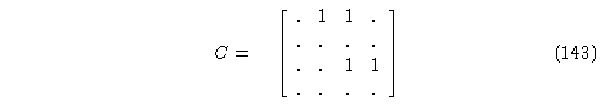
Columnas con suma de elementos diferentes de cero: 1, 2 y 3.
f) Matriz del elemento 1.
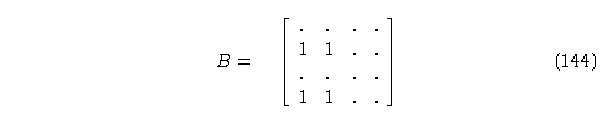
Renglones con suma de elementos diferentes de cero: 1 y 3.
g) Sabemos que la vecindad 22 evoluciona en el pasado con 2, y que la vecindad 21
evoluciona en el pasado con 1 ó 3.
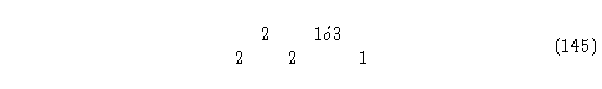
Sin embargo, las vecindades 21 ó 23 deben evolucionar en 2; revisando las matrices de
conectividad, tenemos que la vecindad que cumple este mapeo es 23, por lo tanto, 3 es el
elemento seleccionado.
De esta manera, obtenemos que:
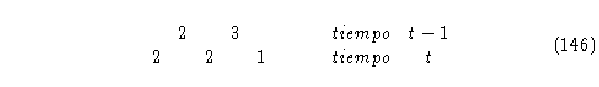
por lo tanto, se concluye que la vecindad 221 evoluciona en el pasado con 3.
Finalmente construimos su regla de evolución inversa ((4,1), cuatro estados un vecino a cada lado) para este autómata, representando sus vecindades en forma matricial con los nodos de su diagrama de de Bruijn.

Para obtener la evolución inversa se debe recorrer ésta medio vecino a la derecha para conservar la paridad con la regla original, ilustrando la evolución de la regla 4h, cuya inversa es la regla 4,1.

Cabe señalar que recurriendo al mismo procedimiento se obtuvo otra regla ((4,t), cuatro estados, 1.5 vecinos a cada lado) que también es inversa a la original, sus vecindades, representadas por los nodos del diagrama de de Bruijn evolucionan hacia atrás como muestra su regla (en forma matricial).

![]()
Seck Tuoh Mora Juan Carlos
E-mail:seck@delta.cs.cinvestav.mx