![]()
El producto cartesiano se puede utilizar, para especificar reglas de evolución de un
ACL, de radio de vecindad h, por ejemplo la regla de evolución de un autómata
(4,h), se pueden formar a través de un producto cartesiano de dos autómatas (2,h) con
sus respectivas reglas. Este producto cartesiano se puede extender para obtener autómatas
(6,h) (producto de un (2,h) por (3,h) y viceversa), (8,h), (10,h) y hasta donde se puedan
calcular (si tiene tiempo) más autómatas con vecindad h.
Si tomamos un autómata (2,h), regla 10; y observemos como evoluciona con una configuración inicial aleatoria.
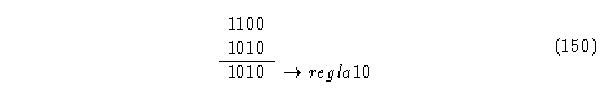
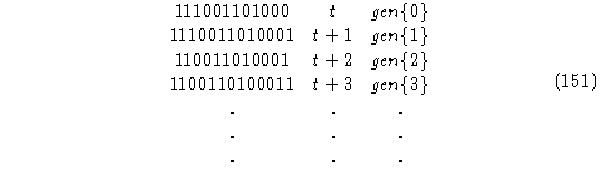
Como podemos ver la evolución de este autómata muestra un corrimiento a la izquierda que es muy característico en un ACLR, por medio de sus matrices de conectividad encontramos que su regla inversa es la regla 12, el cual muestra también un corrimiento a la derecha en su evolución (el contrario de la regla 10).
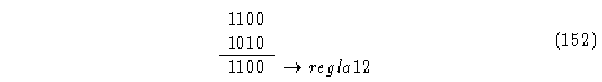
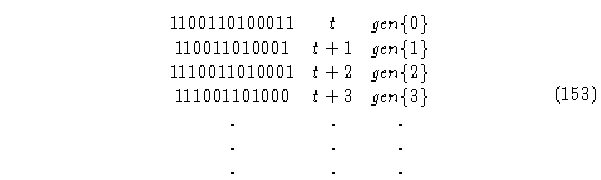
Obtengamos el producto cartesiano de estos dos autómatas.
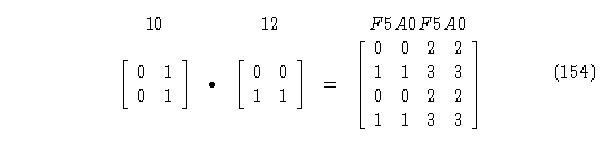
El producto cartesiano se tomó multiplicando cada elemento de la primera matriz por todos los elementos de la segunda matriz, donde
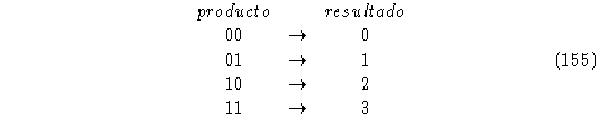
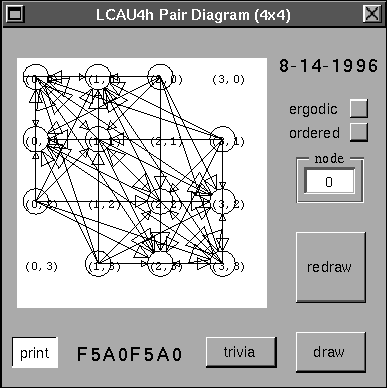
Observemos el diagrama de Parejas del autómata (4,h), regla F5A0F5A0; no existen
ciclos fuera de la diagonal y por lo tanto, puede ser reversible, analicemos una pequeña
evolución de este autómata.
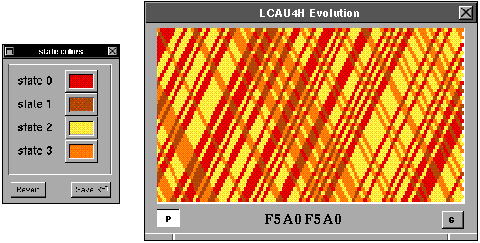
Tenemos que esta evolución es simplemente una mezcla de los corrimientos de los
autómatas (2,h), regla 10 y regla 12. Calculando por medio de las matrices de
conectividad del diagrama de de Bruijn del autómata (4,h), regla F5A0F5A0; se tiene que
la regla inversa es EEEE4444, ahora bien cambiando el orden de multiplicación del
producto cartesiano anterior el resultado es el siguiente:
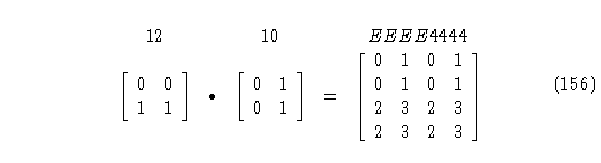
el resultado del producto cartesiano es la regla inversa del autómata (4,h), regla
EEEE4444, analizemos una pequeña evolución de esta regla inversa.
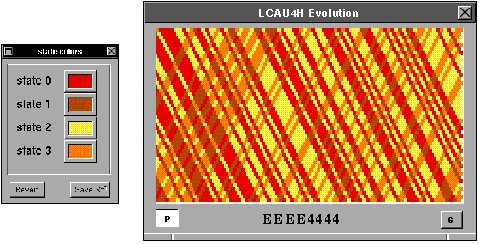
Vemos que el corrimiento de esta evolución es la contraria de la regla F5A0F5A0 y
tambien la combinacion de corrimientos de los autómatas (2,h), regla 12 y regla 10.
Se pueden concluir dos cosas:
![]()
Seck Tuoh Mora Juan Carlos
E-mail:seck@delta.cs.cinvestav.mx