![]()
Un diagrama de de Bruijn es una gráfica en donde los nodos son secuencias de símbolos de algun alfabeto y las ligas de los nodos describen como tales secuencias pueden traslapar para formar otras secuencias.
Los diagramas de de Bruijn surgen cuando N. G. de Bruijn plantea estos diagramas para los procedimientos de los problemas combinatoriales en donde lo que se pretende es encontrar rutas en las que no se repita ninguna conexión. Debido a que las vecindades de los autómatas celulares se presentan en combinaciones que traslapan es posible utilizar estos diagramas para representar el comportamineto de estos.
En el caso de los autómatas celulares los nodos de los diagramas de de Bruijn se construyen a partir de la parte de las vecindades que traslapan con otras, y las ligas entre estos nodos represenatarian a las vecindades que se estan formando entre estos. El número de nodos esta determinado por
![]()
y el número de ligas posibles es igual al número de vecinos debido a la forma en que traslapan estos nodos.[4]
El diagrama de de Bruijn es particularmente útil para el propósito del extendimiento de las propiedades de un vecindario en un autómata celular a las propiedades de las cadenas de celulas porque proporcionan una forma gráfica al tratar con el traslape de las vecindades. Las ligas en los diagramas corresponden a las vecindades, los nodos a los intervalos por los cuales ellas traslapan, y las rutas a traves de los diagramas a las vecindades extendidas o a la secuencia de células en las cuales pueden evolucionar.
Tomaremos como ejemplo al autómata (2,1) donde los nodos posibles son 00, 01, 10 y 11 (0,1,2 y 3 en decimal), el diagrama generico para este automata es:
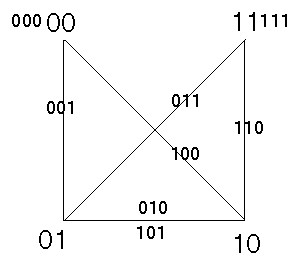
Figure 3.2: Diagrama genérico para el autómata dos-uno que posee 4
nodos, formando a las ocho posibles vecindades
Donde: 00 traslapa con 00 para formar 000
00 traslapa con 01 para formar 001
01 traslapa con 10 para formar 010
01 traslapa con 11 para formar 011
10 traslapa con 00 para formar 100
10 traslapa con 01 para formar 101
11 traslapa con 10 para formar 110
11 traslapa con 11 para formar 111
que son todas las posibles vecindades que hay en el autómata (2,1).
Como se trata de teoría de gráficas es posible representar un diagrama de de Bruijn por medio de una matriz de conexión tal que si hay conexión el elemento de la matriz es 1 y si no hay es 0.
Para un mejor entendimiento del comportamiento de los autómatas las ligas del diagrama de de Bruijn se dibujan con los colores del estado en el que evolucionan.
Asi tendriamos que para la regla 18 de el autómata (2,1) el diagrama de de Bruijn seria:
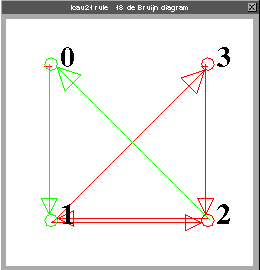
Figure 3.3: Diagrama de de Bruijn para la regla 18
y la siguiente matriz es en la cual los elementos con cero evolucionan en cero los de uno en uno y los que tienen un punto es que no evolucionan para esta regla.
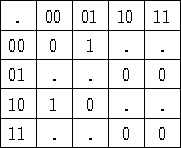
Los diagramas de de Bruijn se diferencian de los diagramas de evolución en el aspecto de que estos solo poseen ciclos y hay tantas ligas permitidas dentro de un nodo como las que salen de él, un número el cual es uniforme para cada nodo. Desde luego que este fino balance puede ser deformado cuando un subdiagrama del diagrama de de Bruijn se cambia, y se presentaria un problema importante el cual seria localizar los ciclos en los cuales han sobrevivido el "podado" con el cual se creo el subdiagrama. Tal diagrama es el diagrama de subconjuntos.
Por lo anterior describiremos a los diagramas de ciclos y a los diagramas de subconjuntos.
![]()