![]()
El diagrama de subconjuntos se forma a partir de los mapeos que hay en el diagrama de de Bruijn, agrupando clases en este diagrama, ya sean clases unitarias, de parejas y las demas que se puedan formar. Es por eso que se le llama diagrama de subconjuntos. En estos diagramas podemos observar que si hay un elemento en la clase unitaria que mapeaba a dos elementos con el mismo estado, en este diagrama mapeará a la pareja que esten formando los dos elementos a los que mapeaba. Aunque pudiera presentarse una confusión porque una pareja de elementos podría mapear a un trío de elementos sin que todos los elementos esten conectados. Aunque las clases pudieran tener matrices individuales de conectividad. Sin embargo, lo antes mencionado implicaría muchos calculos o un congestionamiento bastante grande en el diagrama, lo que lo haría difícil de entender, tomando en cuenta de que se trata de la forma "recortada" del diagrama de subconjuntos puesto que en la forma "completa" se necesitarían mas cálculos y resultaría un diagrama mas comlejo pero mas exacto.[1]
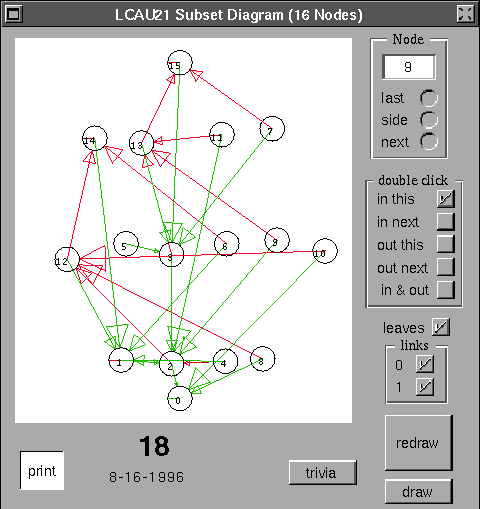
Figure 3.4: Diagrama de subconjuntos para la regla 18 del autómata (2,1)
Para ver si un autómata es sobreyectivo será necesario observar las conexiones que hay entre los subconjuntos, en especial las conexiones del conjunto total con el conjunto vacío. Porque si el subconjunto que contiene a todos los elementos conecta con el conjunto Vacío esto quiere decir que hay al menos un elemento que no tiene ancestros.