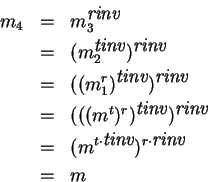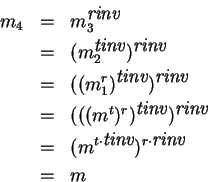


Siguiente: Algoritmos para el logaritmo
Un nivel arriba: Métodos de llave pública
Anterior: En campos finitos
Los elementos de este procedimiento son:
- Mensajes:
- Elementos de
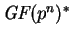 .
.
- Procedimiento:
- El Transmisor elige un
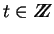 y calcula
y calcula
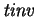 tal que
tal que
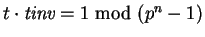 .
El Receptor elige un
.
El Receptor elige un
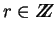 y calcula
y calcula
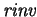 tal que
tal que
 .
Dado el mensaje
.
Dado el mensaje
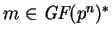 :
:
- 1.
- El Transmisor calcula m1 = mt y envía m1.
- 2.
- El Receptor calcula
m2 = m1r y devuelve m2.
- 3.
- El Transmisor calcula
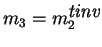 y envía m3.
y envía m3.
- 4.
- El Receptor calcula
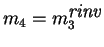 y ha recibido m pues m=m4.
y ha recibido m pues m=m4.
Efectivamente, tenemos que se cumplen las igualdades siguientes:
Un Intruso puede conocer m1= mt,
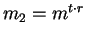 y m3=
mr.
Su tarea, para romper el procedimiento, consiste en calcular bien t
o bien r.
y m3=
mr.
Su tarea, para romper el procedimiento, consiste en calcular bien t
o bien r.
Guillermo Morales-Luna
2000-10-29
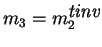 y envía m3.
y envía m3.
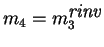 y ha recibido m pues m=m4.
y ha recibido m pues m=m4.