


Siguiente: Algoritmo de Pohlig-Hellman
Un nivel arriba: En anillos de residuos
Anterior: En anillos de residuos
El Algoritmo de Shank resuelve el problema del logaritmo discreto en tiempo
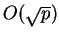 .
En lo que sigue, todas las operaciones aritméticas son hechas en
.
En lo que sigue, todas las operaciones aritméticas son hechas en
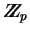 .
Formemos la lista de
.
Formemos la lista de
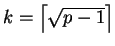 entradas
entradas
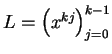 ,
y sea L' la lista de parejas de la forma
(j,xkj),
,
y sea L' la lista de parejas de la forma
(j,xkj),
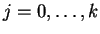 ,
ordenada respecto a su segunda componente.
Formemos ahora la lista
,
ordenada respecto a su segunda componente.
Formemos ahora la lista
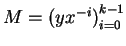 ,
y sea M' la lista de parejas de la forma
(i,yx-i),
,
y sea M' la lista de parejas de la forma
(i,yx-i),
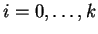 ,
ordenada respecto a su segunda componente.
Sea y0 cualquier elemento, sean j0 la posición en la que aparece y0 en L e i0 la posición en la que aparece y0 en M. La localización de estos índices se hace con los arreglos L' y M'.
El logaritmo discreto de y, respecto a x, es:
,
ordenada respecto a su segunda componente.
Sea y0 cualquier elemento, sean j0 la posición en la que aparece y0 en L e i0 la posición en la que aparece y0 en M. La localización de estos índices se hace con los arreglos L' y M'.
El logaritmo discreto de y, respecto a x, es:
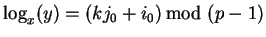 .
En efecto, se tiene
xkj0=y0=yx-i0 y por tanto
y=xkj0+i0.
.
En efecto, se tiene
xkj0=y0=yx-i0 y por tanto
y=xkj0+i0.
Guillermo Morales-Luna
2000-10-29
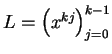 ,
y sea L' la lista de parejas de la forma
(j,xkj),
,
y sea L' la lista de parejas de la forma
(j,xkj),