


Siguiente: En campos finitos
Un nivel arriba: En anillos de residuos
Anterior: Algoritmo de Shank
Con las notaciones anteriores, supongamos factorizado como un producto de primos
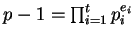 .
Como se quiere conocer el exponente
.
Como se quiere conocer el exponente
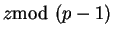 ,
por el Teorema Chino del Residuo, basta calcular
,
por el Teorema Chino del Residuo, basta calcular
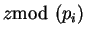 ,
,
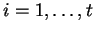 .
Consideremos pues el siguiente problema:
.
Consideremos pues el siguiente problema:
Instancia:
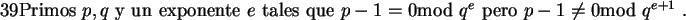
Solución:
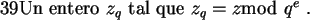
Escribamos a la solución del problema en base q:
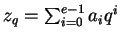 .
Ya que
.
Ya que
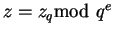 se tiene
z=zq+sqe, para algún
se tiene
z=zq+sqe, para algún
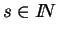 .
Observamos que
.
Observamos que
es decir
![$\frac{1}{q}\left[z_q+sq^e-a_0\right]$](img172.gif) es un entero. Consecuentemente
es un entero. Consecuentemente
Por tanto,
Calculemos pues
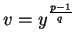 .
Si v=1 entonces a0=0. En otro caso, el mínimo i tal que
.
Si v=1 entonces a0=0. En otro caso, el mínimo i tal que
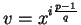 dará el valor de a0.
Si c=1 entonces zq=a0. En otro caso, hacemos
dará el valor de a0.
Si c=1 entonces zq=a0. En otro caso, hacemos
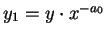 .
Denotemos por z1 al exponente tal que
.
Denotemos por z1 al exponente tal que
 .
De hecho,
.
De hecho,
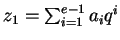 .
Como antes,
.
Como antes,
Calculemos pues
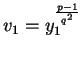 .
Si v1=1 entonces a1=0. En otro caso, el mínimo i tal que
.
Si v1=1 entonces a1=0. En otro caso, el mínimo i tal que
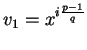 dará el valor de a1.
Si c=2 entonces
zq=a0+a1q. En otro caso, se repite el procedimiento.
dará el valor de a1.
Si c=2 entonces
zq=a0+a1q. En otro caso, se repite el procedimiento.
Figure 3.1:
Algoritmo de Pohlig-Hellman.
|
|



Siguiente: En campos finitos
Un nivel arriba: En anillos de residuos
Anterior: Algoritmo de Shank
Guillermo Morales-Luna
2000-10-29
![\begin{displaymath}z_q+sq^e-a_0=\sum_{i=1}^{e-1} a_i q^i + sq^e=q\left[\sum_{i=0}^{e-2} a_{i+1} q^i + sq^{e-1}\right]\end{displaymath}](img171.gif)
![\begin{displaymath}z_q+sq^e-a_0=\sum_{i=1}^{e-1} a_i q^i + sq^e=q\left[\sum_{i=0}^{e-2} a_{i+1} q^i + sq^{e-1}\right]\end{displaymath}](img171.gif)
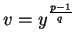 .
Si v=1 entonces a0=0. En otro caso, el mínimo i tal que
.
Si v=1 entonces a0=0. En otro caso, el mínimo i tal que
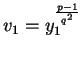 .
Si v1=1 entonces a1=0. En otro caso, el mínimo i tal que
.
Si v1=1 entonces a1=0. En otro caso, el mínimo i tal que
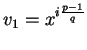 dará el valor de a1.
Si c=2 entonces
zq=a0+a1q. En otro caso, se repite el procedimiento.
dará el valor de a1.
Si c=2 entonces
zq=a0+a1q. En otro caso, se repite el procedimiento.