Teorema Pequeño de Fermat. Si p es primo y
![]() no es divisible entre p, entonces
no es divisible entre p, entonces
![]() .
.
Sean p,q dos números primos, y sea
![]() su producto. Por el teorema de Fermat, se tiene que para cualquier
su producto. Por el teorema de Fermat, se tiene que para cualquier ![]() ,
,
El teorema de Fermat puede plantearse de manera más general. Se dice que dos números enteros n y m son primos relativos si no tienen factores comunes, es decir, si
![]() .
.
La función de Euler es
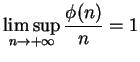 .
.
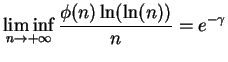 ,
donde
,
donde
Además, dado que la función ``módulo'' es un homomorfismo, se tiene
Consecuentemente, si e,d son enteros tales que
![]() se tiene que:
se tiene que:
![]() .
.
Esta es la base del algoritmo de encriptamiento: Si a es el mensaje, se hace c=ac su cifrado. Entonces, cd=m.
La pareja (n,e) es la llave, que puede hacerse pública.
La llave secreta es (n,d).
Para calcular d sabiendo e, es necesario conocer la factorización
de n como producto de los dos primos p y q.