


Siguiente: Generación de llaves
Un nivel arriba: Algoritmos básicos
Anterior: Algoritmos básicos
De manera aún más restringida, si p y q son primos, n=p q y
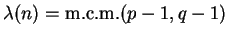 entonces también vale
entonces también vale
Observamos que si se conoce p,q, entonces dado e se calcula, mediante el Algoritmo de Euclides para el Cálculo del Máximo Común Divisor, a su inverso multiplicativo d en el anillo
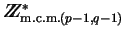 .
Cualquier ataque contra el sistema de encriptamiento tiene como objetivo calcular d.
Los procedimientos de encriptamiento y desencriptamiento mostrados en el algoritmo (4.1) son correctos.
.
Cualquier ataque contra el sistema de encriptamiento tiene como objetivo calcular d.
Los procedimientos de encriptamiento y desencriptamiento mostrados en el algoritmo (4.1) son correctos.
Figure 4.1:
Encriptado y desencriptado RSA.
|
|
Ejemplo. Consideremos dos primos grandes:
p = P23007=262231 y
q = P23008 = 262237. Su producto es entonces
n = p q = 68766670747 el cual número se escribe con un número de bits igual a
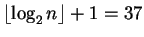 .
Si se toma el exponente e = 12521 se tiene que e es primo relativo con el mínimo común múltiplo de p-1 y q-1. Sea
.
Si se toma el exponente e = 12521 se tiene que e es primo relativo con el mínimo común múltiplo de p-1 y q-1. Sea
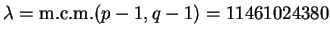 .
De hecho, se tiene
.
De hecho, se tiene
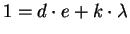 ,
donde
d = 1132280741 y k = -1237.
Para un valor como
m = 1562435 el código correspondiente es
,
donde
d = 1132280741 y k = -1237.
Para un valor como
m = 1562435 el código correspondiente es
y, en efecto, si calculamos la potencia correspondiente al exponente d,
vemos que ésta coincide con el mensaje original m.
Ejemplo. Como un segundo ejemplo, consideremos la cadena de caracteres
Mexicanos al grito de guerra
al tomar uno a uno los caracteres
M , e , x , i , c , a , n , o , s , , a , l , , g , r , i , t , o , , d , e , , g , u , e , r , r , a
y al ponerlos en código ASCII, obtenemos la sucesión de números
77, 101, 120, 105, 99, 97, 110, 111, 115, 32, 97, 108, 32, 103, 114,
105, 116, 111, 32, 100, 101, 32, 103, 117, 101, 114, 114, 97
Al tomarlos de cuatro en cuatro, cada tira de cuatro números se interpreta como un entero, entre 0 y 2564-1, escrito en base 256. Aplicamos pues una conversión de base 256 a base 10. Los 28 caracteres dan 7 números:
Aplicamos a cada uno la función de encriptamiento:
y al aplicar la función de reconversión a base 256
226, 180, 48, 89, 250, 102, 2, 75, 53, 91, 123, 217, 184, 101, 235,
247, 156, 35, 56, 68, 110, 165, 72, 237, 149, 9, 131, 238
que son códigos correspondientes a los caracteres
â , ' , 0 , Y , ú , f ,
no-imprimible
, K , 5 , [ , { , Ù ,
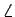
, e , ë ,
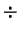
,
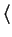
no-imprimible
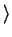
, # , 8 , D , n ,
, H , í ,
no-imprimible
, ,
no-imprimible
, î
â'0Yúf
no-imprimible
K5[{Ù
eë
no-imprimible
#8Dn
Hí
no-imprimible
no-imprimible
î
calculamos la función de desencriptamiento, para obtener
la cual sucesión efectivamente coincide con la ``original''



Siguiente: Generación de llaves
Un nivel arriba: Algoritmos básicos
Anterior: Algoritmos básicos
Guillermo Morales-Luna
2000-10-29