Siguiente: Autentificación Un nivel arriba: Método de llave pública Anterior: Generación de llaves

Pruebas de primacía

Recordamos el famoso

Teorema de los números primos. Consideremos la función que a cada n le asocia el número de primos entre 2 y n inclusive:

$$\pi:n\mapsto \mbox{\rm card}\{m\in [\![2,n]\!]\vert m\mbox{\rm es primo }\}.$$

Entonces ${\displaystyle \lim_{n\to+\infty} \frac{\pi(n)\ln(n)}{n}=1}$.

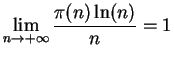Es decir, a la larga, el número de primos entre 2 y n es aproximadamente ${\displaystyle \frac{n}{\ln(n)}}$.

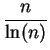De hecho, si p_n es el n-ésimo primo, entonces para n>6: $n\ln n < p_n < n(\ln n+\ln \ln n)$.

Ahora bien, atendiendo al Teorema Pequeño de Fermat, dado n, se dice que $a\in[\![1,n]\!]$ es un testigo según Fermat de que n es compuesto si $a^{n-1}\not=1\mbox{\rm mod }n$. n es seudoprimo según Fermat respecto a $a\leq n-1$ si $a^{n-1}\not=1\mbox{\rm mod }n$.

Naturalmente, si p es primo entonces p es seudoprimo según Fermat respecto a cualquiera de los enteros que lo preceden.

Ejemplo. El número $341=11\cdot 31$ es seudoprimo según Fermat respecto a 100 enteros que lo preceden.

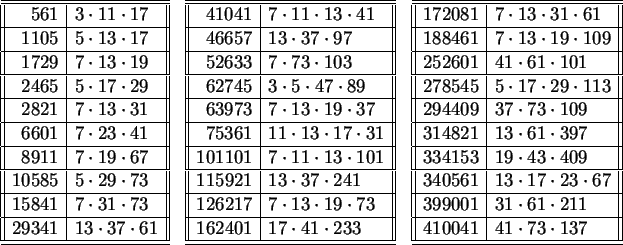
En efecto, la función $c:Z\!\!\!Z_{341}\to Z\!\!\!Z_{341}, a\mapsto a^{340}\mbox{\rm mod }341$ tiene como imagen al conjunto $\{1,56,67,253\}$. De hecho, la imagen inversa de 1, llamémosla c₃₄₁^-1 consta de los números enlistados en la tabla 4.1,

  

Table: Conjunto c₃₄₁^-1: Imagen inversa de 1 bajo $a\mapsto a^{340}\mbox{\rm mod }341$.

y este conjunto puede expresarse como la unión de 19 órbitas de funciones de la forma $k\mapsto a^{k}\mbox{\rm mod }341$, mostradas en la tabla 4.2,

  

Table 4.2: Orbitas cuya unión forma c₃₄₁^-1.

Si n es compuesto y no posee testigos de que sea compuesto, es decir, si

$$\forall a\in[\![2,n-1]\!]:\ \mbox{\rm m.c.d}(a,n)=1\ \Rightarrow\ a^{n-1}=1\mbox{\rm mod }n.$$ (4.1)

se dice que n es de Carmichael.

Hecho. n es de Carmichael si y sólo si se cumplen las siguientes dos condiciones siguientes:

• n está libre de cuadrados, es decir: $\forall p: \left[p\vert n\ \Rightarrow\ p^2\not\vert n\right]$.
• $\forall p: \left[p\vert n\ \Rightarrow\ (p-1)\vert(n-1)\right]$.

En la tabla 4.3 presentamos una lista de los primeros 30 números de Carmichael.

  

Table 4.3: Primeros 30 números de Carmichael. Al lado de cada uno se presenta su factorización como producto de primos.

Se tiene pues que un número de Carmichael supera la prueba de primacía de Fermat, mas no es primo.

Otra prueba de primacía, ésta más fuerte, se debe al siguiente

Hecho. Si n es un primo impar, escribamos n-1=2^s r, donde r es impar. Entonces para todo a<n tal que $\mbox{\rm m.c.d.}(a,n)=1$ se tiene

$$a^r\mbox{\rm mod }n=1 \hspace{3em}\mbox{\rm o bien}\hspace{3em} \exists t<s:a^{2^tr}\mbox{\rm mod }n=-1$$ (4.2)

Un número n se dice ser un seudoprimo fuerte si satisface la condición (4.2) para todo a<n tal que $\mbox{\rm m.c.d.}(a,n)=1$.

Más aún, para cada n, sea

$$% latex2html id marker 4349 W(n)=\{a<n\vert\mbox{\rm m.c.d.}(a,n)=1\ \&\ \neg\mbox{\rm (\ref{ec.strpri})}\}$$

Así pues, n es seudoprimo fuerte si y sólo si $W(n)=\emptyset$.

Si $W(n)\not=\emptyset$ y $a\in W(n)$, se dice que a es un testigo de que n es compuesto, es decir, de que no es primo.

En tanto se prueben más a's y ninguno atestigüe que n es compuesto, mayor será la certeza de que n es primo. Este es el algoritmo de Miller-Rabin para revisar si acaso el número dado n es primo. Si t es el número de a's probadas, la probabilidad de que declare a un número n (fuerte seudo-)primo, siendo que n sea compuesto, es decir, la probabilidad de que el algoritmo se equivoque, al declarar a un número como primo, es menor que $\left[\frac{1}{4}\right]^t$. Los parámetros de entrada del algoritmo de Miller-Rabin son n y t y da como respuesta una decisión de si acaso n es seudoprimo o no.

Un procedimiento de búsqueda aleatoria para generar primos grandes está dado por el algoritmo 4.4.

  

Figure 4.4: Algoritmo de búsqueda aleatoria para generar primos grandes.

Siguiente: Autentificación Un nivel arriba: Método de llave pública Anterior: Generación de llaves