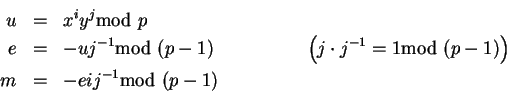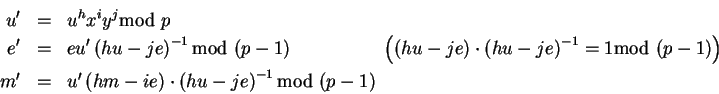


Siguiente: Digital Signature Standard
Un nivel arriba: Diversos esquemas de autentificación
Anterior: Esquema RSA
Recordamos que todo usuario posee una llave pública
(pU,xU,yU) y una llave secreta zU, donde p es primo, xU es un elemento primitivo de
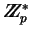 e
e
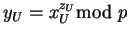 .
Se tiene pues:
Un intruso S que conociese el mensaje m buscaría generar los correspondientes coeficientes (u,e) de la firma.
Si conociese u, el exponente e podría conocerse calculando
.
Se tiene pues:
Un intruso S que conociese el mensaje m buscaría generar los correspondientes coeficientes (u,e) de la firma.
Si conociese u, el exponente e podría conocerse calculando
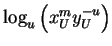 .
Si conociese e, el elemento u podría conocerse tratando de reslver la ecuación:
.
Si conociese e, el elemento u podría conocerse tratando de reslver la ecuación:
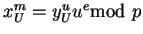 .
Algún otro intento consistiría en tratar de calcular simultáneamente u,e. No se conoce de un algoritmo eficiente que lo haga. Tampoco se ha demostrado que no exista tal algoritmo.
Sn embargo, de manera aleatoria un intruso podría generar mensajes firmados: Sean
.
Algún otro intento consistiría en tratar de calcular simultáneamente u,e. No se conoce de un algoritmo eficiente que lo haga. Tampoco se ha demostrado que no exista tal algoritmo.
Sn embargo, de manera aleatoria un intruso podría generar mensajes firmados: Sean
![$i,j\in [\![0,p-2]\!]$](img315.gif) tales que j y p-1 sean primos relativos. Definamos:
tales que j y p-1 sean primos relativos. Definamos:
Entonces (u,e) es una firma de m con la llave pública (p,x,y).
En efecto, módulo p valen las igualadades siguientes:
Un segundo procedimiento para generar firmas legítimas sobre ciertos mensajes es el siguiente:
Supongamos conocido unmensaje m con su firma correspondiente (u,e). Sean
![$h,i,j\in [\![0,p-2]\!]$](img318.gif) tales que hu-je y p-1 sean primos relativos. Definamos:
tales que hu-je y p-1 sean primos relativos. Definamos:
Entonces (u',e') es una firma de m' con la llave pública (p,x,y).

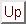


Siguiente: Digital Signature Standard
Un nivel arriba: Diversos esquemas de autentificación
Anterior: Esquema RSA
Guillermo Morales-Luna
2000-10-29
![$\begin{array}[t]{rcl}
u &=& x_U^{k}\mbox{\rm mod }p \\
e &=& \left(m-z_U u\right)k^{-1}\mbox{\rm mod }(p-1) %
\end{array}$](img309.gif) ¡Atención! Si se mostrase k entonces podría calcularse la llave secreta zU a partir de la firma:
¡Atención! Si se mostrase k entonces podría calcularse la llave secreta zU a partir de la firma:
![$\begin{array}[t]{rcl}
u &=& x_U^{k}\mbox{\rm mod }p \\
e &=& \left(m-z_U u\right)k^{-1}\mbox{\rm mod }(p-1) %
\end{array}$](img309.gif) ¡Atención! Si se mostrase k entonces podría calcularse la llave secreta zU a partir de la firma:
¡Atención! Si se mostrase k entonces podría calcularse la llave secreta zU a partir de la firma: