


Posterior: Presentación
algebraica Arriba: Algebras
booleanas Anterior: Algebras
booleanas
Definición 3.1 Todo retículo acotado
y distributivo tal que todo elemento posee un complemento se dice ser
un ´
ALGEBRA BOOLEANA.
Por el lema 1.2.2 se tiene que si  es un álgebra booleana entonces la función complemento
es un álgebra booleana entonces la función complemento  ,
, 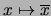 está bien definida. Nos
referiremos pues a un álgebra booleana enlistando todas sus
componentes:
está bien definida. Nos
referiremos pues a un álgebra booleana enlistando todas sus
componentes: 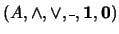 .
.
Por ejemplo, si  es un conjunto,
es un conjunto, 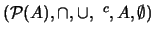 es un álgebra
booleana. Ésta se dice ser el ´ALGEBRA DE
SUBCONJUNTOS.
es un álgebra
booleana. Ésta se dice ser el ´ALGEBRA DE
SUBCONJUNTOS.
Ejemplo 3.1 (Álgebra de finitos-cofinitos)
Sea
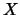
un conjunto cualquiera (por ejemplo
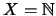
). Sea
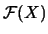
la
colección de todos los subconjuntos de
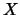
que o
bien son finitos o bien son complementos de finitos en
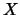
.
Evidentemente
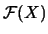
es cerrada bajo las operaciones
de

, así como también
posee al conjunto vacío y al ``universo''
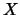
.
Por tanto
es un álgebra
booleana. Ésta se dice ser el ´
ALGEBRA DE
SUBCONJUNTOS FINITOS-COFINITOS.
En otras palabras, un término booleano es una expresión
que puede evaluarse en un álgebra booleana.
En otras palabras, el término dual de cualquier término
booleano se obtiene al intercambiar las constantes y los operadores de
unión e inter.
Observación 3.1 (Principio de dualidad) Si
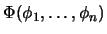
es una aseveración que se
cumple en toda álgebra booleana, entonces

también vale en toda
álgebra booleana.
En efecto, si 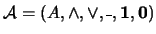 es un álgebra booleana, entonces
es un álgebra booleana, entonces 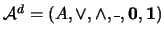 es también un álgebra booleana y el enunciado
es también un álgebra booleana y el enunciado 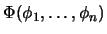 válido en
válido en  equivale a que el enunciado
equivale a que el enunciado  vale en
vale en 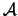 .
.
Proposición 3.1 En
toda álgebra booleana
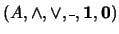
se
cumplen las relaciones siguientes:
- Leyes de De Morgan.
-
 :
:
- Principio de la doble negación.
-
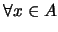 :
: 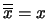 .
.
Demostración
Leyes de De Morgan: Probemos la primera identidad. Ya que los
complementos son únicos, basta ver que
Para la primera de estas igualdades, observamos que
La segunda de estas igualdades se sigue similarmente. La segunda Ley
de De Morgan se sigue aplicando el principio de dualidad a la primera.
Principio de la doble negación: Éste se sigue de
la unicidad de los complementos. 
Definición 3.4 Un álgebra booleana

se dice ser
COMPLETA si
cualquier subconjunto en ella posee un supremo y un ínfimo.
Por ejemplo el álgebra de suconjuntos finitos-cofinitos sobre 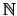 no es completa. En efecto, sea
no es completa. En efecto, sea  la mónada que consiste del
la mónada que consiste del  -ésimo
número par. El supremo de la colección
-ésimo
número par. El supremo de la colección 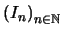 debería ser el
conjunto de todos los pares pero éste ni es finito ni es
cofinito. Por tanto no puede pertenecer a
debería ser el
conjunto de todos los pares pero éste ni es finito ni es
cofinito. Por tanto no puede pertenecer a 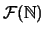 .
. 
Definición 3.5 Un ´
ATOMO en un álgebra booleana

es un
elemento minimal entre sus elementos no-nulos, es decir, distintos de

. El álgebra booleana

se dice
ser
ATÓMICA si es la
unión de los conos superiores de sus átomos.
Ejemplo 3.2 Un conjunto
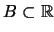
es
SEMI-BORELIANO si se puede expresar como la unión de
intersecciones de intervalos semi-infinitos de la forma
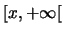
o de complementos de ellos. Sea

la colección de conjuntos semi-borelianos. Entonces

es un álgebra booleana que no posee
átomos.
Proposición 3.2 Toda álgebra booleana
que sea completa y atómica puede identificarse con el
álgebra de subconjuntos correspondiente a su conjunto de
átomos.
Demostración
Tan sólo bosquejaremos la demostración de esta
proposición y dejaremos al lector la tarea de suplir los
detalles omitidos.
Sea  un álgebra booleana, completa y
atómica. Denotemos por
un álgebra booleana, completa y
atómica. Denotemos por 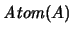 a su conjunto de átomos. Para cada
elemento
a su conjunto de átomos. Para cada
elemento  consideremos el conjunto
consideremos el conjunto 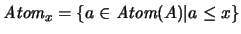 de
átomos ``por debajo'' de
de
átomos ``por debajo'' de  . La
correspondencia
. La
correspondencia 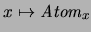 es uno a uno, pues
es uno a uno, pues 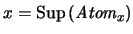 , y es
suprayectiva, pues
, y es
suprayectiva, pues  es completa. Más
aún, puede verse que esta correspondencia ``preserva las
operaciones''.
es completa. Más
aún, puede verse que esta correspondencia ``preserva las
operaciones''. 
En este curso sólo nos ocuparemos de álgebras booleanas
completas y atómicas. Ahora bien si el conjunto de
átomos es finito, digamos 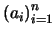 , entonces a cada átomo
, entonces a cada átomo 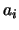 lo podemos identificar con el vector básico
lo podemos identificar con el vector básico 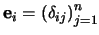 donde
donde  es la delta de Kroenecker. Y al supremo
de un conjunto de átomos lo identificamos con el supremo de los
vectores básicos correspondientes a esos átomos.
Así, a la postre estamos identificando a la álgebra
booleana de
es la delta de Kroenecker. Y al supremo
de un conjunto de átomos lo identificamos con el supremo de los
vectores básicos correspondientes a esos átomos.
Así, a la postre estamos identificando a la álgebra
booleana de  átomos con el hipercubo de
dimensión
átomos con el hipercubo de
dimensión  .
.
Definición 3.6 La
LONGITUD de un álgebra completa y atómica es el
número de átomos en ella.
En otras palabras, la longitud de un álgebra completa y
atómica es la dimensión del hipercubo con el cual se
identifica. Ahora bien, el hipercubo tiene una rica estructura
algebraica. Para finalizar este capítulo haremos un repaso de
estas nociones.



Posterior: Presentación
algebraica Arriba: Algebras
booleanas Anterior: Algebras
booleanas
Guillermo
Morales-Luna
2004-07-27
![\begin{eqnarray*}
\left[x\land y\right] \lor \left[\overline{x}\lor \overline{y...
...eft[\mbox{\bf 1}\lor \overline{x}\right] \\
&=& \mbox{\bf 1}
\end{eqnarray*}](img175.png)