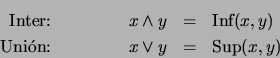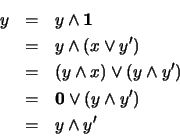


Posterior: Algebras
booleanas Arriba: Estructuras
algebraicas básicas Anterior: Conjuntos ordenados
Definición 2.1 Sea
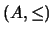
un conjunto ordenado.

es un
RET´i
CULO
INFERIOR si cualquier pareja de elementos en

posee un ínfimo.

es un
RET´i
CULO
SUPERIOR si cualquier pareja de elementos en

posee un supremo.

es un
RET´i
CULO, a secas, si

es, a la vez, un
retículo inferior y un retículo superior.
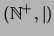 es un retículo. Pero el conjunto
unión de los divisores de
es un retículo. Pero el conjunto
unión de los divisores de  y de
y de 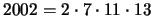 , que tiene
, que tiene 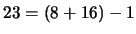 elementos, es un retículo inferior que no
es superior.
elementos, es un retículo inferior que no
es superior.
Si  no es vacío, entonces su conjunto de partes
no es vacío, entonces su conjunto de partes 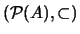 es un retículo.
es un retículo.
Sea 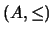 un retículo. Para cualesquiera
un retículo. Para cualesquiera  escribamos
escribamos
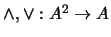 son pues operaciones binarias definidas en
son pues operaciones binarias definidas en  .
.
Observación 2.1 Es evidente que las
operaciones
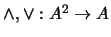
poseen las siguientes propiedades:
- Asociatividad.
-
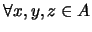 :
:
- Conmutatividad.
-
 :
:
- Idempotencia.
-
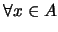 :
:
- Absorción.
-
 :
:
- Criterio de comparación.
-
 :
:
Las operaciones del retículo se obtienen del orden en el
conjunto ordenado. También puede procederse al revés,
según se enuncia en la siguiente
Proposición 2.1 Sea
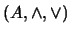
una estructura algebraica tal que
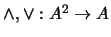
son operaciones binarias asociativas,
conmutativas, idempotentes y que satisfacen las relaciones de ``orden''
definidas arriba. Entonces, la relación definida como
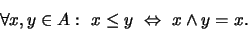 |
(1) |
es de orden, con la cual
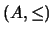
es un retículo
cuyas operaciones de unión e inter son precisamente
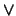
y
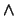
.
La demostración de esta proposición es directa de las
definiciones y por ende la asignamos al lector. Primero hay que ver que
la relación definida por (1)
es, en efecto, reflexiva, transitiva y simétrica. Luego hay que
ver que dados dos elementos  ,
,  es el ínfimo de esa pareja y
es el ínfimo de esa pareja y 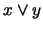 es el
supremo.
es el
supremo. 
Ejemplo 2.1 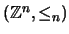
es un retículo con las
operaciones
![$\land:(\mbox{\bf x},\mbox{\bf y}) \mapsto \left[\min(x_j,y_j)\right]_{j=1}^n$](img100.png)
y
![$\lor:(\mbox{\bf x},\mbox{\bf y}) \mapsto \left[\max(x_j,y_j)\right]_{j=1}^n$](img101.png)
.
En este ejemplo, puede verse que si dos vectores 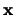 ,
, 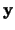 no son comparables en
no son comparables en 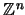 , entonces los segmentos
, entonces los segmentos  y
y  son las diagonales principales de un rectángulo de
dimensión
son las diagonales principales de un rectángulo de
dimensión  con aristas paralelas a los ejes de
coordenadas.
con aristas paralelas a los ejes de
coordenadas. 
Demostración
1. Supongamos 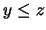 . Se tiene:
. Se tiene: 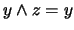 . Luego:
. Luego:
por tanto, 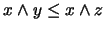 . Similarmente:
. Similarmente: 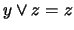 . Luego:
. Luego:
por tanto, 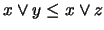 .
.
2. Para probar esa desigualdad hay que ver que 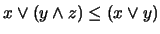 y también que
y también que 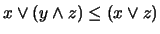 . Pero estas dos desigualdades
se siguen inmediatamente del punto 1.
. Pero estas dos desigualdades
se siguen inmediatamente del punto 1.
3. Estas desigualdades se prueban similarmente a las de 2. 
Definición 2.2 Sea
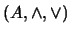
un retículo. Diremos que

está
ACOTADO INFERIORMENTE si
posee un elemento mínimo, al que denotaremos por

. Diremos que

está
ACOTADO
SUPERIORMENTE si posee un elemento
máximo, al que denotaremos por
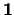
.

está acotado si lo está tanto inferior como
superiormente.
Por ejemplo 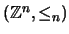 no está acotado de ninguna
manera.
no está acotado de ninguna
manera.
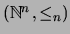 está acotado inferiormente y el
elemento mínimo es
está acotado inferiormente y el
elemento mínimo es ![$\mbox{\bf0}=[0, 0, \ldots, 0]$](img122.png) .
.
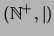 está acotado inferiormente, y su
elemento mínimo es el número 1, es decir
está acotado inferiormente, y su
elemento mínimo es el número 1, es decir 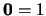 . En ese retículo, para cada
. En ese retículo, para cada  el cono inferior
el cono inferior  consistente de todos los divisores de
consistente de todos los divisores de  forma un
subretículo acotado. En él, el mínimo es
forma un
subretículo acotado. En él, el mínimo es 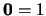 y el máximo es
y el máximo es  .
. 
Naturalmente, si 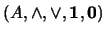 es un retículo
acotado entonces
es un retículo
acotado entonces 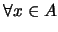 :
: 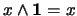 y
y 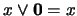 . Es decir,
. Es decir, 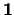 y
y  son unidades de los operadores inter y
unión respectivamente.
son unidades de los operadores inter y
unión respectivamente.
Definición 2.3 Sea
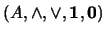
un retículo
acotado y sea

un elemento cualquiera. Un elemento
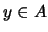
se dice ser un
COMPLEMENTO
de

si se cumplen las relaciones siguientes:
 |
(2) |
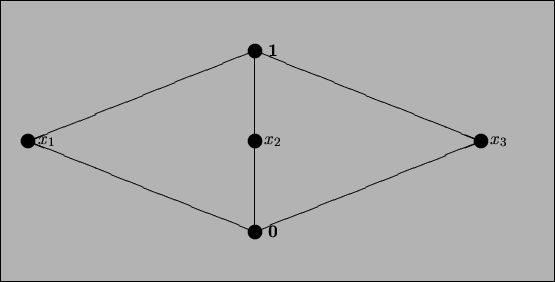
En algunos retículos puede suceder que un elemento posea
más de un complemento. En la figura 1.1 bosquejamos un retículo en
el que cada elemento ``en la parte media'' es complemento de cualquiera
otro en esa misma parte.
Figure 1.1: Retículo
con elementos que poseen varios complementos.
 |
Por otro lado, es evidente que si  es complemento de
es complemento de  entonces también
entonces también  es complemento de
es complemento de  . Asímismo,
. Asímismo,  es
complemento de
es
complemento de 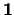 .
.
Para citar otro ejemplo, en 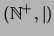 consideremos
consideremos  y su cono inferior
y su cono inferior  de divisores. Si
de divisores. Si 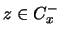 es tal que
es tal que 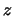 y
y  son primos relativos, es decir no poseen divisores comunes
distintos de 1, entonces
son primos relativos, es decir no poseen divisores comunes
distintos de 1, entonces 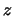 y
y  son
complementos, uno del otro, en el retículo
son
complementos, uno del otro, en el retículo  .
. 
Definición 2.4 Un retículo
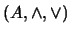
se dice ser
DISTRIBUTIVO si posee la propiedad siguiente:
Distributividad. 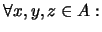
Las nociones de distributividad y complementariedad están muy
ligadas según se ve en el siguiente:
Lema 2.2 Sea
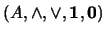
un retículo
acotado tal que cada elemento posee un complemento. Si

es
distributivo entonces cada elemento de

posee un
único complemento.
Demostración
Supongamos  distributivo. Sea
distributivo. Sea  . Veamos que
cualesquiera dos complementos de
. Veamos que
cualesquiera dos complementos de  han de coincidir.
En efecto, si
han de coincidir.
En efecto, si  y
y 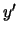 satisfacen las relaciones de
complementariedad (2) entonces:
satisfacen las relaciones de
complementariedad (2) entonces:
Mutatis mutandi obtenemos 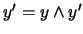 y en
consecuencia
y en
consecuencia  .
.



Posterior: Algebras
booleanas Arriba: Estructuras
algebraicas básicas Anterior: Conjuntos ordenados
Guillermo
Morales-Luna
2004-07-27