

Posterior: Lecturas recomendadas
Arriba: Estructuras algebraicas básicas
Anterior: Homomorfismos
Ultraproductos
Sea
 un conjunto no-vacío. Un filtro
un conjunto no-vacío. Un filtro  sobre
sobre 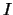 será un filtro en el álgebra booleana de las partes de
será un filtro en el álgebra booleana de las partes de 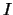 ,
,
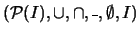 .
Sea
.
Sea
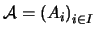 una colección de conjuntos no-vacíos indicada con índices en
una colección de conjuntos no-vacíos indicada con índices en 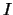 y sea
y sea
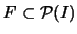 una colección de conjuntos en
una colección de conjuntos en 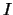 . Denotamos por
. Denotamos por
al producto cartesiano de los elementos en 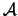 . Ahí definimos la relación siguiente:
. Ahí definimos la relación siguiente:
Se tiene que si  es un filtro sobre
es un filtro sobre 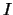 , entonces
, entonces 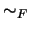 es una relación de equivalencia.
En efecto, supongamos que
es una relación de equivalencia.
En efecto, supongamos que  es un filtro. Como
es un filtro. Como 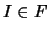 , para cada
, para cada
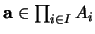 ,
,
 , es decir,
, es decir, 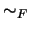 es reflexiva. Ahora como la igualdad en cada conjunto
es reflexiva. Ahora como la igualdad en cada conjunto  es simétrica,
es simétrica, 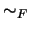 también lo es. Finalmente, dado que la intersección de elementos en
también lo es. Finalmente, dado que la intersección de elementos en  está también en
está también en  ,
, 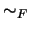 es transitiva.
Si se piensa a los elementos en el filtro
es transitiva.
Si se piensa a los elementos en el filtro  como ``conjuntos grandes'' entonces se puede pensar a la relación
como ``conjuntos grandes'' entonces se puede pensar a la relación 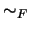 como una relación de igualdad ``casi en todas partes'' y escribiremos en ocasiones:
como una relación de igualdad ``casi en todas partes'' y escribiremos en ocasiones:
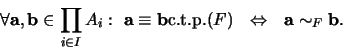 |
(1) |
El cociente
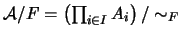 se dice ser el PRODUCTO REDUCIDO por
se dice ser el PRODUCTO REDUCIDO por  . Si todos los conjuntos
. Si todos los conjuntos  coinciden el producto reducido se dice ser una POTENCIA REDUCIDA.
Para cada
coinciden el producto reducido se dice ser una POTENCIA REDUCIDA.
Para cada
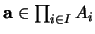 denotamos por
denotamos por
 a la clase de equivalencia de
a la clase de equivalencia de 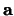 bajo la relación
bajo la relación 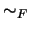 .
Ahora, supongamos que en cada conjunto
.
Ahora, supongamos que en cada conjunto  se tiene una relación
se tiene una relación 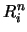 de aridad
de aridad  . Definamos la relación
. Definamos la relación 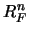 en
en
 haciendo
haciendo
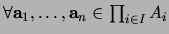 :
:
 |
(2) |
Observamos que 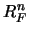 es congruente con la relación
es congruente con la relación 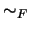 , es decir:
, es decir:
![\begin{displaymath}
\left[\forall j\leq n: \mbox{\bf a}_j\sim_F \mbox{\bf a}_j'...
...box{\bf a}_1',\ldots,\mbox{\bf a}_n'\right)\in R_F^n\right].
\end{displaymath}](img422.png) |
(3) |
En efecto, para cada 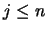 escribamos
escribamos
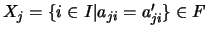 y sea
y sea
 . Si
. Si 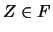 , al ser
, al ser  un filtro, entonces la intersección de estos conjuntos está en
un filtro, entonces la intersección de estos conjuntos está en  :
:
 . Evidentemente
. Evidentemente
por tanto
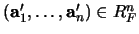 .
Así pues, de manera más apropiada, diremos que la estructura
.
Así pues, de manera más apropiada, diremos que la estructura
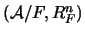 es el producto reducido, por el filtro
es el producto reducido, por el filtro  , de las estructuras
, de las estructuras
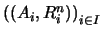 .
Si
.
Si  es un ultrafiltro el producto reducido por
es un ultrafiltro el producto reducido por  se dice ser un ULTRAPRODUCTO y si todos los
se dice ser un ULTRAPRODUCTO y si todos los  coinciden y coinciden también las relaciones
coinciden y coinciden también las relaciones 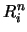 entonces el ultraproducto se dice ser una ULTRAPOTENCIA.
entonces el ultraproducto se dice ser una ULTRAPOTENCIA.



Posterior: Lecturas recomendadas
Arriba: Estructuras algebraicas básicas
Anterior: Homomorfismos
Guillermo Morales-Luna
2004-07-27